Можно привести различные доводы, чтобы объяснить, почему снизилась величина пробега. На ум приходит холодная погода (возможно, в горах), низкое качество бензина, езда на короткие расстояния, смена водителя, большая загрузка, плохие свечи зажигания. Последний довод был выбран в качестве единственного объяснения. Новые свечи вернули величину пробега к ее историческому значению.
Указывает ли восстановление средней величины пробега на то, что именно свечи зажигания были источником проблемы? Полной уверенности в этом нет. Просто, когда подобная ситуация произойдет с другим транспортным средством, мы включим свечи зажигания в перечень возможных причин.
Грузо– и пассажироперевозчики в США (2 млн) в большинстве своем аккуратно ведут учет пройденных миль и закупленного числа галлонов топлива. Они могли бы использовать эти данные более успешно. Для обнаружения проблем водитель мог бы ежедневно вести для каждой машины простую карту хода процесса. Возможно, это занятие понравится водителю и откроет массу возможностей для него и владельца.
Контрольная карта указывает на существование причин вариаций, которые лежат вне системы. Саму причину она не раскрывает.
Карта хода процесса – это не мгновенный индикатор. Тренд из шести последовательных точек или серия из семи или восьми точек ниже или выше среднего значения обычно указывают на присутствие особой причины (см. ссылку далее).
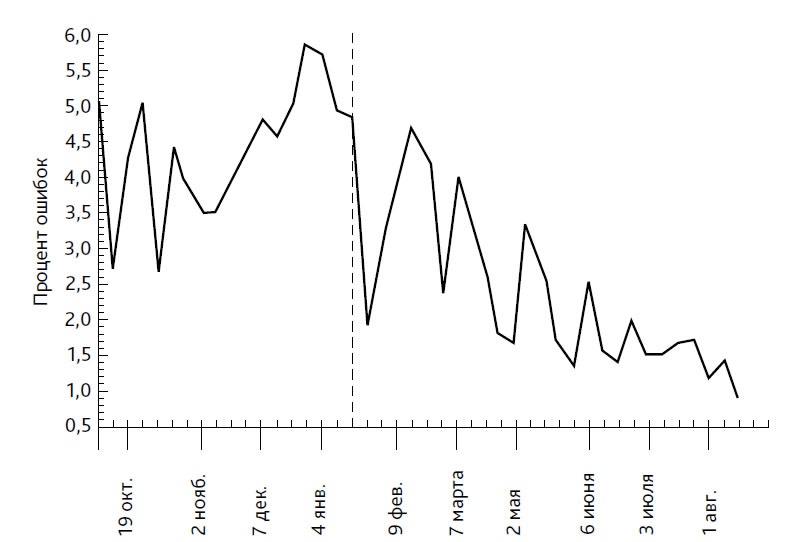
Рис. 31. Фрагмент карты хода процесса для числа миль на галлон между заправками топливного бака. Серия из девяти точек ниже среднего говорит об изменении процесса. Причина в плохих свечах зажигания. (Этот пример предоставлен г-ми Франком Белчамбером и Робертом Джеймсоном из Nashua Corporation.)
Первый урок применения статистической теории. Курсы по статистике часто начинаются с изучения распределений и их сравнения. Студентов ни на занятиях, ни в книгах не предупреждают о том, что для аналитических целей (таких как улучшение процесса) распределения и вычисление среднего, определение метода, стандартного отклонения, значений хи-квадрат, t-статистики и т. д. бесполезны, если только данные не были получены для процесса в состоянии статистической управляемости. Соответственно, первый шаг при исследовании данных – понять, получены ли они в состоянии статистической управляемости. Самый легкий путь при анализе данных – это расположить точки в порядке их появления, чтобы понять, можно ли извлечь какую-либо пользу из распределения, образованного данными
[76].
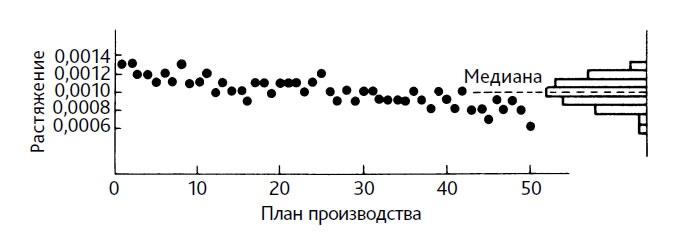
Рис. 32. Карта хода процесса для 50 пружинок, испытанных в порядке их изготовления. Если не учитывать время изготовления, данные образуют симметричное распределение, но если расположиmь их в порядке изготовления пружин, окажется, что распределение бесполезно. Например, распределение не сказало бы нам, в какой допуск могут попасть готовые пружинки. Причина в том, что здесь не существует идентифицируемого процесса
В качестве примера обратимся к распределению, которое, по-видимому, имеет наилучшие характеристики, но при этом не просто бесполезно, а вводит в заблуждение. На рис. 32 показано распределение результатов замеров 50 пружинок одного вида, используемых в фотоаппарате определенного типа. Пружинки измерялись растяжением под действием силы 20g. Распределение выглядит довольно симметричным и не выходит за пределы допуска. Возникает искушение сделать вывод, что процесс находится в удовлетворительном состоянии.
Однако значения растяжений, расположенные в порядке времени их изготовления, демонстрируют тренд в сторону уменьшения. Что-то не так с процессом изготовления или с измерительным прибором.
Любая попытка использовать распределение, показанное на рис. 32, бесполезна. Например, расчет стандартного отклонения для данного распределения не даст значения, которое можно использовать для предсказания. Оно ничего не говорит о процессе, поскольку он нестабилен
[77].
Таким образом, мы получили очень важный урок – для анализа данных нужно посмотреть на них. Откладывайте точки в порядке производства изделий или в каком-то ином разумном порядке. Для некоторых проблем полезна простая диаграмма рассеяния.
Что, если кто-либо попытается использовать это распределение для расчета показателей воспроизводимости процесса? Он попадет в ловушку, из которой сложно выбраться. Процесс нестабилен. Ему вообще нельзя приписать никакой воспроизводимости. То же самое мы наблюдали при анализе рис. 2.
Распределение (гистограмма) всего лишь демонстрирует накопленные данные работы процесса, ничего не говоря о его воспроизводимости. Как мы увидим, процесс обладает воспроизводимостью, только если он стабилен. Воспроизводимость процесса достигается и подтверждается путем использования контрольной карты, но не самим распределением. Как мы уже видели, и простая карта хода процесса дает представление о воспроизводимости процесса.
Какая характеристика или характеристики важны? Какие значения важны? Какие надо изучать с помощью контрольной карты, а какие – любым другим методом? Ответ зависит от предметной области (проектирование, химия, психология, знание процесса, знание материалов и т. д.). В любом случае следует использовать статистическую теорию.
Особые и общие причины. Распространенная ошибка при интерпретации наблюдений состоит в предположении, что каждое событие (дефект, ошибка, несчастный случай) можно соотнести с кем-то (обычно с тем, кто находится под рукой) или увязать с некоторым конкретным событием. Дело в том, что большинство проблем сферы услуг и производства связаны с системой. Иногда дефект действительно локален и его можно приписать некомпетентности или лености работника. Мы будем называть дефекты системы общими причинами, а дефекты, связанные с преходящими, быстротечными событиями, особыми причинами.
Термин общие причины для системных дефектов был впервые использован, насколько мне известно, примерно в 1947 г. в разговоре с д-ром Гарри Альпертом (ныне покойным) на тему бунтов в тюрьмах. В литературе термин впервые появился в 1956 г.
[78]




