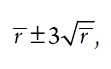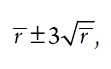
где r – среднее число остановок шпинделя за месяц. В эту формулу заложено допущение о том, что остановки независимы: остановка одного шпинделя не влияет на другие остановки ни этого шпинделя, ни какого-либо другого, а кроме того, она не снижает вероятность возникновения того же дефекта где бы то ни было.
Шпиндель, попадающий за верхний предел, требует пристального внимания. Его остановка может быть результатом особенностей его эксплуатации или свидетельством потребности в экстренной наладке. Шпиндель, выходящий за нижний предел, – это либо супершпиндель, либо он эксплуатировался в особенных условиях. Шпиндели, которые не выходят за указанные границы, являются обычными, ожидающими своей очереди в процессе регулярного обслуживания.
Заметит ли читатель те же самые ошибки в нижеприведенных правилах обслуживания самолетов?
1. Аварийные уровни устанавливаются с помощью методов, применяемых в отрасли. Для справки см. документ Управления гражданской авиации CAP 418 и циркуляр Комитета по анализу техобслуживания и ремонта при Федеральном управлении гражданской авиации за 1971 г.
2. Метод требует вычисления среднего по фактической интенсивности замен на 1000 посадок за последние 12 периодов времени плюс два стандартных отклонения.
3. Стандартное отклонение – статистический параметр, отражающий вариабельность относительно среднего значения.
4. Аварийный уровень для трех периодов вычисляется по четырем ежеквартальным значениям интенсивности замен на 1000 посадок.
Верным шагом, предшествующим любым вычислениям, было бы нанесение любым способом данных на график, например в виде еженедельной карты хода процесса. Даже такой грубый инструмент, как распределение времени до отказа, мог бы обнаружить определенные структуры и дать полезную информацию относительно отказов компонент.
Эксперимент Монте-Карло с воронкой
[82]. Если начать настраивать стабильный процесс, пытаясь скомпенсировать нежелательные результаты или гонясь за сверхвысокими результатами, ситуация на выходе станет хуже, чем если бы процесс протекал без вмешательств (приписывается Уильяму Лацко).
Распространенный пример – принятие корректирующих мер в связи с появлением дефектного изделия или жалобы от потребителя. Результатом усилий по улучшению будущего выхода (предпринимаемых из лучших побуждений) будет удвоение вариаций на выходе или даже разрушение системы. Для совершенствования системы требуется не вмешательство, а ее фундаментальное изменение.
Цель эксперимента с воронкой – продемонстрировать, что зарегулированность ведет к потерям. В это нелегко поверить. Для эксперимента требуется лишь имеющаяся в каждом доме кухонная утварь. Нужны: 1) воронка; 2) мраморный шарик, который может пройти в отверстие воронки; 3) стол; 4) держатель для воронки. На рис. 35 наглядно показана схема эксперимента. Требуемые шаги:
1. Нанести мишень на поверхность стола, над ней расположить воронку.
2. Бросить шарик сквозь воронку.
3. Отметить точку, где шарик остановится.
4. Бросить шарик снова сквозь воронку. Отметить точку, где он остановится.
5. Сделать не менее 50 бросков.
Перед тем как сделать шаг 4 и совершить последующие броски, вы должны установить правило регулировки (наладки) воронки. Человечество изобрело четыре правила.

Рис. 35. Результаты падения шарика сквозь воронку с использованием описанных в тексте четырех правил. Показаны только удаленные точки, чтобы избежать перегруженности рисунка
Правило 1. Зафиксировать воронку строго над мишенью, никак ее не регулируя.
Правило 2. На броске номер k (k = 1, 2, 3, …) шарик остановится в точке zk – это измеренное нами расстояние от точки остановки до цели. (Другими словами, zk – это ошибка падения в k-й точке.) Передвиньте воронку на расстояние zk от ее последней позиции. (Система с памятью.)
Правило 3. Установите воронку над точкой zk, отсчитываемой от цели. (Система без памяти.)
Правило 4. Установите воронку прямо над той точкой zk, где шарик остановился последний раз. (Система без памяти.)
Используя правила 2 и 3, оператор пытается сделать все возможное, чтобы скомпенсировать предыдущую неудачу.
Результаты
[83]:
Правило 1. Это, безусловно, наилучший выбор. Правило 1 приводит к стабильному распределению точек. Оно дает минимальный разброс (минимальную дисперсию) для любого диаметра окружности, описанной вокруг цели.
Правило 2. В результате применения правила 2 возникает стабильный выход, но ожидаемая дисперсия точек распределения внутри любого диаметра окружности, описанной вокруг цели в два раза больше, чем дисперсия, ожидаемая для правила 1.
Правило 3. Система неустойчива. В конце концов шарик падает все дальше и дальше от цели, образуя симметричную структуру.
Правило 4. Система неустойчива. Шарик падает с каждым разом все дальше от цели в одном направлении.
В результате применения правил 3 и 4 система оказывается нестабильной, и эта нестабильность нарастает.
Правило 4 приводит к случайным блужданиям. Точные попадания шарика напоминают попытки пьяного человека добраться до дома, который падает после каждого шага и плохо понимает, где какая сторона света. Он сбивается с направления, не помня предыдущих шагов. В конце концов он все больше удаляется от цели.