Иногда естественная защитная реакция не дает нам даже помыслить о каких бы то ни было переменах. Поэтому внедрять что-либо новое всегда очень сложно.
2.6.3.5. Если на предыдущих этапах ограничение было снято, возвращайтесь к шагу 1
Избавляясь от имеющегося ограничения, вы неизбежно вызываете к жизни следующее. Речь может идти о возможности улучшения производительности еще на пару или на десятки процентов, но потом вы найдете еще одно ограничение. Это вовсе не проблема, это естественный подход к совершенствованию системы: концентрируйте внимание на текущем ограничении системы. Вот самая оптимальная стратегия.
Далее следует предостережение: не позволяйте инерционности управленческого мышления становиться ограничением системы.
2.6.4. ПРОЦЕСС ЛОГИЧЕСКИХ РАССУЖДЕНИЙ ПО ТОС
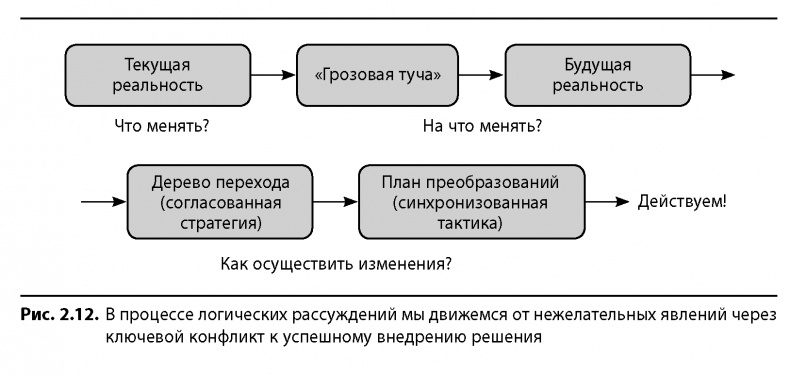
На рис. 2.12 представлена общая схема процесса и основных методов логических рассуждений по ТОС. Голдратт выстроил процесс таким образом, чтобы он давал ответы на три вопроса:
1. Что менять?
2. На что менять?
3. Как осуществить изменения?
Этапы процесса связаны между собой таким образом, что результат одного служит входной информацией для следующего.
Голдратт разработал и инструменты для реализации данного процесса. Помимо выполнения своей определенной роли в общем ряду каждый из них может применяться и самостоятельно (кроме деревьев текущей и будущей реальности). Далее приводится описание каждого, однако затем практически до самого конца книги об использовании большинства из них говорить мы не будем, чтобы книга была интересна и тем, кто заинтересован не столько в изучении теории ограничений, сколько в способах совершенствования управления своими проектами. Широко применяться будет диаграмма разрешения конфликтов «грозовая туча» — самый лучший из всех инструментов ТОС, пригодных к самостоятельному использованию. В последней главе показано, как использовать процесс логических рассуждений для создания ССРМ. Полное описание и свод правил по применению процесса логических рассуждений даны у Детмера [23].
Многих сперва пугает инструментарий логических рассуждений ТОС и соответствующие сокращения. Большинству требуется две-три недели усиленного обучения и тренировок, чтобы начать использовать инструменты ТОС самостоятельно, и годы практического опыта, чтобы достичь настоящего мастерства в этом деле. Как отмечают Эрик Норин, Дебра Смит и Джеймс Макей [26], даже после подобного обучения лишь ограниченное число людей способно вырабатывать серьезные решения. (Исследование было опубликовано довольно давно, процесс обучения и сами инструменты с тех пор претерпели некоторые изменения. Более свежих данных у меня нет, однако по личным наблюдениям могу сказать, что сделанные выводы до сих пор актуальны.)
Чтобы успешно применять ССРМ, не требуется досконального знания всех инструментов ТОС. Дальнейшее описание в этой главе приводится, чтобы показать, что ССРМ была тщательно разработана и подвергнута критическому осмыслению и лишь потом испытывалась в реальных ситуациях.
Дерево текущей реальности
Дерево текущей реальности (ДТР) — схема причинно-следственных связей существующей системы, где нежелательные явления (НЯ) восходят к некоему ключевому конфликту. Если отнести все (или большинство) НЯ к одному ключевому конфликту, будет найдена точка оптимального приложения сил, то есть мы сможем определить, что следует менять. Рекомендации по анализу (выражаясь словами Поппера, «критическому обсуждению») ДТР ведут к тому, чтобы команда согласилась с представленной логикой причин и следствий, вызвавших проявление НЯ. Иными словами, люди приходят к единой точке зрения на то, в чем же заключается настоящая проблема. В ДТР определяется, какие политики, системы оценок, правила поведения действуют в существующей реальности. ДТР становится предметом критического обсуждения. Его цель — помочь команде отточить логику рассуждений, найти общий язык и заручиться поддержкой заинтересованных лиц. ДТР читается снизу вверх с использованием утверждений вида «если... то».
Диаграмма разрешения конфликтов «грозовая туча»
Диаграмма «грозовая туча» в совокупности с правилами ее преподнесения и использования помогает найти и реализовать решение конфликта или дилеммы. Это построение жестко заданной горизонтальной формы показывает необходимые условия перехода от одного логического утверждения к другому. Диаграмма читается слева направо с использованием формулировок, передающих эту логику: «Чтобы наступило событие х, нужно, чтобы соблюдалось условие у».
Разработанная Голдраттом диаграмма может быть эффективным инструментом для вскрытия глубинных убеждений, верований, лежащих в основе конфликтов и дилемм, хотя бессознательные установки найти нелегко даже при помощи данного инструмента.
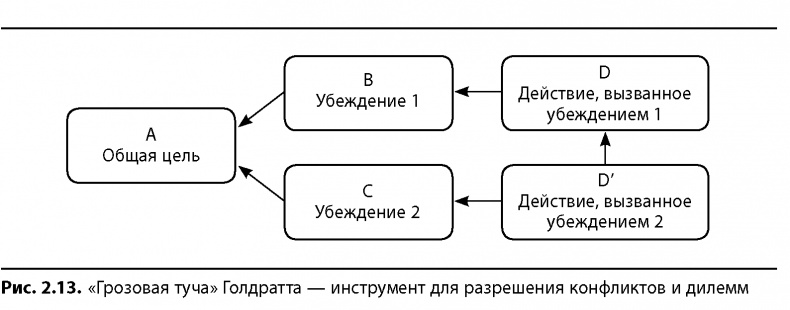
На рис. 2.13 представлен общий вид диаграммы «грозовая туча», состоящей из убеждений и действий. (Я пришел к выводу, что это основной вид представления данной логической схемы.) Диаграмма отображает две точки зрения на реальность, или два аргумента (в смысле — логических). Представим себе блоки D и D' как два противоположных представления о способе достижения цели. Аргумент первый гласит: «Чтобы получить А, надо иметь В. Чтобы получить В, надо иметь D». Второй аргумент выглядит так: «Чтобы получить А, надо иметь С. Чтобы получить С, надо иметь D'». Таким образом, мы видим два логических способа достижения одной и той же цели. Убеждения могут и не противоречить друг другу, но действия являются совершенно противоположными. Иначе и конфликта бы не возникло.
Процесс «рассеивания грозовой тучи» столь же важен, сколь и процесс ее построения. Обычно диаграмму рисует одна из конфликтующих сторон, ясно представляющая себе, какие именно точки зрения вступили в противоречие (то есть знающая, в чем заключаются D и D'). Тот, кто рисует схему, как правило, может понять, какое именно убеждение легло в основу появления его точки зрения. Однако он может лишь догадываться, какие установки кроются за мнением оппонентов. (Как уже говорилось ранее, ни одна из сторон может вообще не осознавать действия своих убеждений.) Автор диаграммы представляет ее вниманию другой стороны, зачитывая сначала часть схемы, имеющую отношение к оппонентам. При этом он четко оговаривает, что блок С — это лишь его предположение и оно обсуждается. После зачитывается другая сторона диаграммы и в заключение говорится: «Неудивительно, что возникло разногласие». Затем докладчик предлагает: «Давайте найдем решение, обеспечивающее А, В и С без реализации D и D'. При таком раскладе выиграют все. Попробуем выявить установки, лежащие в основании связей в диаграмме, и посмотрим, можно ли опровергнуть одну или более и найти решение, выигрышное для всех».




