В следующих разделах мы рассмотрим каждый из данных пунктов подробно.
Для эффективного применения ССРМ в отдельном проекте крайне необходимо добиться следующих изменений привычного стиля работы:
1) руководство должно способствовать тому, чтобы при оценке операций давались средние величины, и не требовать от исполнителей завершения работ в точно обозначенные сроки;
2) руководство должно дать исполнителям возможность в конкретный момент времени заниматься только одним заданием;
3) исполнители должны сосредотачивать усилия на одной операции и передавать результаты на следующий этап, как только работа завершена;
4) чтобы решить, над чем дальше работать, каждый должен использовать план проекта и отчеты по буферу.
Вот и все!
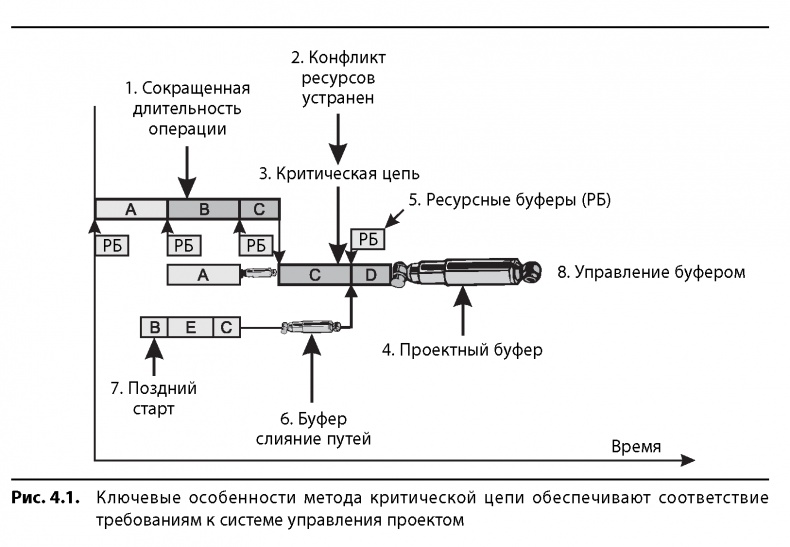
4.2. Разработка решения «критическая цепь»
Следующие разделы описывают характеристики метода критической цепи в свете пяти направляющих шагов ТОС. Не знаю, таким ли путем Голдратт на самом деле пришел к пониманию этих особенностей. В соответствии с приведенными у Поппера [2] описаниями теории познания и научного метода вовсе не важно, как именно Голдратт нашел эти характеристики (что Поппер назвал бы «дерзкой гипотезой»). Важно то, что мы должны подвергнуть данную гипотезу критическому обсуждению, проверить экспериментально и посмотреть, будут ли результаты свидетельствовать в пользу предпочтения критической цепи критическому пути.
4.2.1. ОПРЕДЕЛЕНИЕ ОГРАНИЧЕНИЯ В ПРОЕКТЕ
Очевидным ограничением в проекте является цепочка операций, на выполнение которых уйдет больше всего времени. РМВОК называет ее критическим путем — это «последовательность работ в графике, определяющая продолжительность проекта». Как указано далее в РМВОК, СРМ — это «метод анализа сети расписания, используемый для определения возможной гибкости при планировании (возможного временного резерва) в различных логических путях в сети расписания проекта и определяющий минимальную общую длительность проекта. Ранний старт и ранний финиш рассчитываются с помощью прямого прохождения, исходя из указанной даты начала. Поздний старт и поздний финиш рассчитываются с помощью обратного прохода, исходя из указанной даты завершения, которой иногда бывает ранний финиш проекта, рассчитанный с помощью прямого прохождения».
В этих определениях не уточняется несколько важных моментов. Во-первых, предположение о том, что длительность операции определяется точно и с первого раза (детерминирована). Во-вторых, не указано, с какой вероятностью сделана оценка (50% и более высокая степень вероятности?). А ведь это весьма существенно.
В РМВОК идет речь и о вероятностных подходах к составлению расписания проекта, таких как методы PERT и Монте-Карло. Однако определения даются очень скудные, так что пользоваться этими методами, исходя только из описаний в РМВОК, невозможно. Как показали мои исследования, реально на практике они применяются редко.
Чтобы выполнить любую операцию проекта, необходимы две составляющие: результаты предыдущей операции и исполнитель. (Для самой первой операции на проекте предыдущим этапом может быть просто разрешение на начало работ.) В определении критического пути не затрагиваются возможные ограничения по ресурсам. Только в неявном виде потребность в ресурсах иногда учитывается и при нахождении критического пути, поскольку при оценке длительности операции предполагается определенный уровень доступности ресурсов. При определении критического пути не учитывается в полной мере ограниченность ресурсов на выполнение операций и не допускается нарушение логики хода работ, то есть «прыжки» с одной логической цепочки операций на другую запрещены.
Базовое определение критической цепи заключается просто в нахождении ограничения проекта, или «последовательности зависимых событий, не позволяющих проекту завершиться за меньшее время. При нахождении критической цепи зависимость от ресурсов такая же, как и зависимость между операциями».
Поиск ограничений проекта в расписании связан с тем, что расписание влияет и на бюджет, и на содержание проекта. К независимым переменным, сказывающимся на результате, относятся проектное задание (содержание), установленная система управления проектом, а также ресурсы, которые доступны для работы по проекту. Результаты управления проектом — величины взаимозависимые (фактические содержание, бюджет и сроки). Когда увеличивается длительность при неизменном содержании, обычно растут и затраты. Если расширяется содержание без изменений имеющегося бюджета (или количества ресурсов), как правило, сдвигается график. А когда содержание расширяется, но сроки должны остаться неизменными, вырастут расходы. Следовательно, правильным будет в первую очередь сосредоточиться на своевременном выполнении проекта.
Планирование проекта методом критического пути базируется на скрытой установке, согласно которой приемлемым способом справиться с потенциальным ограничениям в ресурсах будет нахождение критического пути с последующим выравниванием загрузки ресурсов. Специалисты в построении сетевых диаграмм знают, что оптимального метода выравнять ресурсы не существует. Некоторые алгоритмы дают заведомо слабые результаты. Другие подходы к распределению нагрузки также не отличаются эффективностью, обычно из-за лежащих в их основе алгоритмов расчета. В большинстве диаграмм применение схем выравнивания ресурсов приводит к увеличению сроков. Поэтому в очень немногих проектах используются инструменты для выравнивания ресурсов.
Читая курс для членов PMI, я провел небольшое исследование. Среди слушателей много сертифицированных профессионалов в управлении проектами РМР. Практически все они согласны с тем, что получить в свой проект ресурс именно в тот момент, когда он необходим, очень трудно и часто из-за этого случаются задержки. Однако мало кто (менее 5%) указывает, что регулярно занимается выравниванием ресурсов (то есть учитывает ограниченность ресурсов на проекте). Когда я интересуюсь причинами, большинство объясняет, что после выравнивания ресурсов срок реализации превышает ожидания руководства.
На рис. 4.2 изображен типичный график, построенный методом критического пути. Имена исполнителей на нем указывают на уникальные ресурсы. Очевидно, что не удастся уложиться в срок, поскольку исполнитель не может выполнять несколько заданий одновременно.
На рис. 4.3 расположение операций изменено, чтобы снять пересечение в ресурсах. Аналогично схемам, действующим во многих компьютерных программах для выравнивания ресурсов, сначала мы назначаем исполнителей на цепочку, по которой запас свободного времени минимальный, обычно это первоначальный критический путь. Обратите внимание: после этого по всем цепочкам возникает резерв, то есть критического пути — пути с нулевым запасом времени — больше нет. (Компьютерные программы по-разному поступают с данным результатом. Некоторые оставляют первоначально найденный критический путь, другие помечают как критическую только самую последнюю операцию. Как в подобных программах выглядит критический путь потом, когда по ходу проекта он, по идее, должен меняться, я не знаю.)



