На рисунке 6 наглядно представлено статистическое распределение. Маленькие кубики, показывающие число измерений, располагаются вдоль горизонтали в соответствии с измеряемыми значениями. Совокупность таких кубиков и образует фигуру, называемую гистограммой.
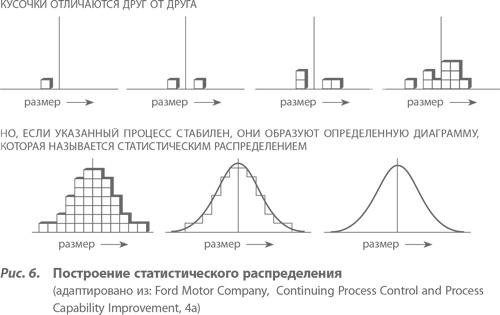
Предположим, мы регистрируем все больше и больше данных (и, соответственно, подстраиваем вертикальную ось, чтобы гистограмма не вылезала за верх страницы). Тогда при некоторых существенных условиях, которые обсуждаются ниже, общая картинка стабилизируется и изменения в ней с приходом все новых и новых измерений будут практически незаметны. Она становится графическим представлением статистического распределения результатов измерений. Этот рисунок характеризует возможное поведение разброса результатов измерений. Данные и распределение на рисунке 6 интерпретировались как размеры некоторых образцов, но они могут точно так же интерпретироваться в контексте всех примеров, приводившихся выше, как и в миллионах других примеров.
Ключевая фраза для понимания рисунка 6 – «если сам исходный процесс стабилен» – напрямую связана с понятием статистически управляемого процесса. Идея заключается в том, что если в ходе измерений на процессы оказывает влияние некоторое постороннее воздействие (например, по отношению к приведенным выше примерам: настройка машины изменилась, норма обслуживания для механика по наладке увеличилась, вы сели на диету, ваш поставщик стал использовать сырье плохого качества и т. д.), то результаты измерений не могут рассматриваться как происходящие из одного и того же источника, и, таким образом, никакое стабильное распределение нельзя использовать для его представления. На самом деле, как мы увидим позже, определение стабильности, представляемое единственным фиксированным распределением, слишком идеализировано с практической точки зрения (позже мы будем ссылаться на эту искусственно-идеальную ситуацию как на представляющую идеально точную стабильность).
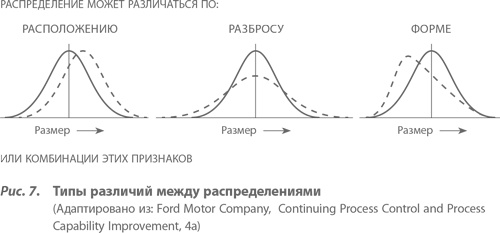
Как видно из рисунка 7, распределения могут отличаться во многих отношениях. Термин «положение» относится к положению среднего значения, «разброс» характеризует степень вариабельности относительно среднего, а «форма» указывает, например, расположены ли данные значения симметрично относительно среднего или, напротив, есть некоторые сжатия с одной стороны и растяжения с другой.
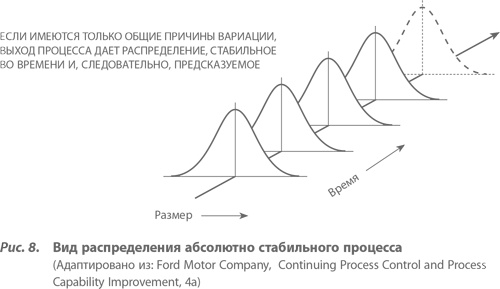
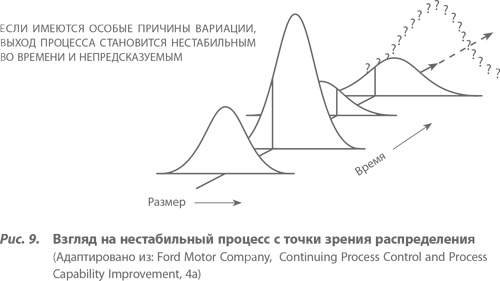
В терминах статистического распределения рисунки 8 и 9 соответственно определяют, так сказать, на глаз, что подразумевается под процессами, находящимися и не находящимися в статистически управляемом состоянии.
Процесс находится в состоянии статистического контроля (статистически управляемый процесс), если лежащее в его основе распределение остается практически неизменным во времени. Если же распределение изменяется во времени существенно и непредсказуемо, то говорят о процессе, вышедшем из-под контроля (ставшем неуправляемым).
Как ученый, Шухарт знал: во всем, что поддается измерению, обязательно есть вариации. Вариации могут быть крайне большими, ничтожно малыми или находиться между этими двумя крайностями, но они есть всегда
[21].
Исследования Шухарта по статистическому управлению процессами вдохновлялись его наблюдениями за характером вариации в изучаемых им производственных процессах. Часто их характер отличался от того, что Шухарт видел в так называемых «естественных» процессах (под последними он понимал, например, такое явление, как броуновское движение). На стр. 5 книги Дональда Дж. Уиллера и Дэвида С. Чамберса «Понимание статистического управления процессом» (Understanding Statistical Process Control) эти два важных наблюдения объединяются следующим образом:
«Несмотря на то что все процессы проявляют вариабельность (изменчивость), в некоторых из них вариации контролируемые (управляемые), а в других – неконтролируемые (неуправляемые)».
В частности, Шухарт часто находил контролируемые (стабильные) вариации (представленные на рисунках 5а, 5b) в естественных процессах, а неконтролируемые (нестабильные) вариации (такие, как на рисунках 5с, 5d и 9) – в производственных процессах. Различия в них ясны. В первом случае мы знаем, чего можно ожидать в терминах изменчивости: процесс находится в статистически управляемом состоянии (состоянии статистического контроля); во втором случае мы этого не знаем: процесс статистически неуправляем (находится в статистически неконтролируемом состоянии). Если в первом случае мы можем предсказать будущее с некоторыми шансами на успех, то во втором мы этого сделать не можем.
Теперь проясним, что в данном контексте имеется в виду под «предсказанием». Мы не думаем, что способны точно спрогнозировать, какими именно будут следующие значения процесса. Традиционные статистики иногда говорят о «точечных оценках», или «точечных предсказаниях», – так может создаться впечатление, будто подобная точность достижима. Но то, что они делают на самом деле, – это получение некоторых ожидаемых средних значений. Кроме того, нам нужны также знания о вариациях вокруг этих средних, чтобы узнать нечто вразумительное о возможных будущих значениях.
Давайте обобщим три наиболее значимые предпосылки, о которых мы узнали выше.
Во-первых, если выход процесса определяется влиянием особых причин, то его поведение меняется непредсказуемо и, таким образом, невозможно оценить результат изменений в конструкции, обучении, политике закупок комплектующих и т. д., которые менеджмент мог бы ввести в этот процесс (или в систему, которая содержит этот процесс) с целью улучшения. Пока процесс находится в неуправляемом состоянии, никто не может предсказать его возможности. Это и есть та мысль, которую я тщетно старался довести до сведения компании, «внедрившей статистический контроль».
Во-вторых, когда особые причины устранены, так что остаются только общие, тогда улучшения могут зависеть от управляющих воздействий. Поскольку в этом случае наблюдаемые вариации системы определяются тем, каким образом были спроектированы и построены процессы и система, только управляющий персонал, менеджеры имеют полномочия для изменений системы и процессов. Как часто говорит Майрон Трайбус, директор американского Института качества и производительности, «люди работают в системе. Задача менеджера – работать над системой, улучшая ее с их помощью»
[22].






