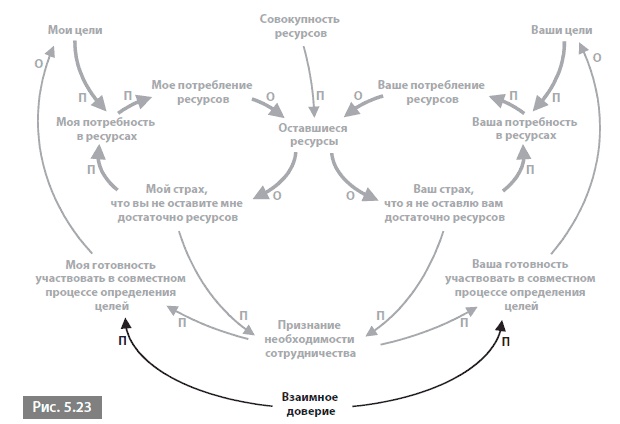
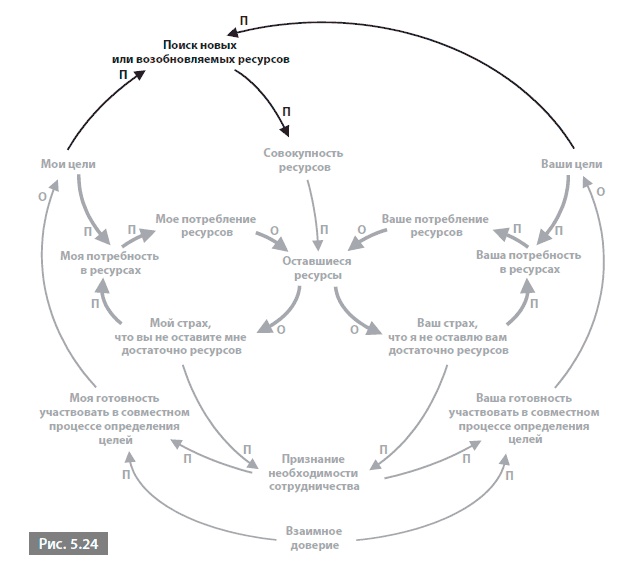
Эта окончательная диаграмма цикличной причинности представляет собой сложную, но я уверен, что совершенно понятную, сеть из шести взаимосвязанных петель: двух первоначальных усиливающих петель и четырех дополнительных уравновешивающих. Каждый элемент на этой диаграмме относится хотя бы к одной петле за исключением взаимного доверия. Это единственное свободное звено, и его присутствие или отсутствие движет всей системой.
Это история о том, как две усиливающие петли, связанные через общее пользование ресурсами, могут вести к конфликту, но мы рассмотрели еще три различных способа управления ситуацией. В каждом из них появились две дополнительные уравновешивающие петли, действующие в соответствии с проводимой политикой. Два способа были направлены на поиск способов урегулирования конфликта путем изменения правил распределения дефицитных ресурсов, а один – на изменение правил создания спроса на них. Однако все три способа действуют по одному принципу: две уравновешивающие петли нарушают экспоненциальный рост двух усиливающих петель.
Более подробно мы рассмотрим взаимодействие усиливающих и уравновешивающих петель в главе 8. А в главе 6 мы изучим поведение второго строительного элемента – уравновешивающей петли.
6. Постановка задач и выбор целей
Более подробно об уравновешивающих петлях
На рис. 6.1 показана уравновешивающая петля, которую мы уже рассматривали: диаграмма цикличной причинности, описывающая, как налить чашку кофе.
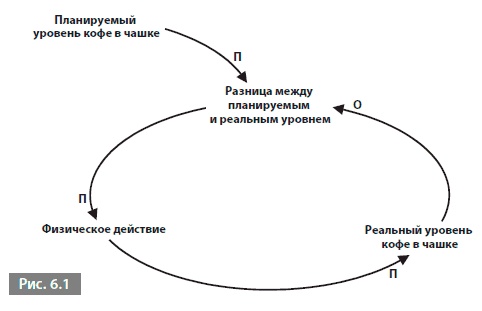
Как ведет себя эта петля?
Вспомните эту петлю и убедитесь в том, что понимаете ее, особенно все связи типа П и О. Предположив, что я наливаю кофе осторожно, нарисуйте график, демонстрирующий поведение реального уровня кофе в чашке во времени.
Мы видим нечетное число связей типа О, следовательно, это уравновешивающая петля, где реальный уровень кофе в чашке стремится к планируемому. Если я наливаю кофе осторожно, то поведение реального уровня кофе в чашке во времени выглядит, как на рис. 6.2.
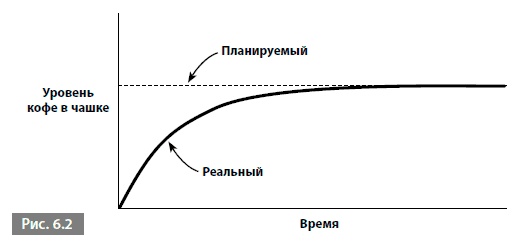
Как можно заметить, уровень кофе в чашке неуклонно приближается к планируемому, и, когда цель достигнута, система не меняется в течение неопределенного периода времени.
А что произойдет, если я буду наливать кофе не очень осторожно?
Представьте себе, что я на секунду отвлекся, пока наливал кофе в чашку. Что произойдет? Какие действия я предприму? Как они будут связаны с диаграммой цикличной причинности? И как тогда будет выглядеть график поведения реального уровня кофе в чашке?
Это не такое простое упражнение, особенно третий вопрос, касающийся диаграммы цикличной причинности, поэтому хорошенько подумайте.
Как вы помните, в качестве планируемого уровня кофе у нас задано полчашки, поэтому, если я отвлекусь хотя бы на секунду, я налью больше, но, вероятно, замечу это прежде, чем кофе перельется через край. Что произойдет дальше? Я осторожно наклоню чашку и вылью лишний кофе, но если я опять буду неосторожен, то могу наклонить ее слишком сильно, и тогда мне придется опять доливать кофе. В конце концов, переливая кофе туда-сюда, я добьюсь нужного мне уровня.
Как эти действия будут связаны с диаграммой цикличной причинности? Начнем с того момента, когда я заметил, что налил кофе больше половины чашки, и остановился. В этот момент реальный уровень кофе в чашке выше планируемого. Если я определю разницу между планируемым и реальным уровнем как планируемый уровень минус реальный, то получу отрицательное число. Причем чем больше я превышу уровень, тем большим будет это отрицательное число. Двигаясь по петле, мы увидим, что связь типа П, соединяющая разницу между планируемым и реальным уровнем и физическое действие, демонстрирует движение эти двух элементов в одном направлении. По мере того как разница между планируемым и реальным уровнем все больше уходит «в минус», то же самое происходит и с физическим действием. Но что может означать «отрицательное физическое действие»? Если положительное физическое действие означает наливание кофе в чашку, то отрицательное может означать только одно: выливание из чашки. Получается, что диаграмма цикличной причинности предвосхищает события и говорит нам, что делать: отрицательное значение разницы между планируемым и реальным уровнем подсказывает нам, что кофе надо выливать.
Это тоже связь типа П, связывающая физическое действие с реальным уровнем кофе в чашке, поэтому, если физическое действие является отрицательным, его влияние на реальный уровень кофе в чашке тоже отрицательное. Это подразумевает уменьшение реального уровня, что, конечно же, верно, поскольку мы выливаем кофе из чашки.
Предупреждение: далее следует часть, которую многие считают слишком сложной. Диаграмма цикличной причинности показывает связь типа О между реальным уровнем кофе в чашке и разницей между планируемым и реальным уровнем. Это означает, что они движутся в противоположных направлениях. Поэтому если реальный уровень кофе в чашке уменьшается, разница между планируемым и реальным уровнем должна увеличиваться, стремиться «в плюс», то есть становиться «более положительной» (как вы помните, вначале она была отрицательной). Если это число увеличивается и становится все «более положительным», оно должно становиться «менее отрицательным» и приближаться к нулю.
Система опять стремится к цели наполнить чашку наполовину.
Перечитайте предыдущую страницу
Мало кто понимает это с первого раза. Поэтому не спеша перечитайте все еще раз. Смысл в том, что при строгом описании поведения петли всем элементам приписаны количественные значения, и все они имеют знак «плюс» или «минус». Обычно когда они имеют знак «плюс», мы не задумываемся об этом или даже не замечаем этого. Во всех предыдущих примерах подразумевалось, что все элементы имеют знак «плюс». Это первый пример, где некоторые элементы имеют знак «минус», и бывает трудно сообразить, что, когда вы увеличиваете отрицательное число (скажем –3), вы делаете его более положительным (оно становится –2), а не более отрицательным (оно не становится –4).

