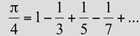Результаты и необходимые меры. Это именно тот случай, когда анализ показал свою неэффективность. В досужих рассуждениях об этой истории частенько проскальзывали разные предположения – например, что магазинах пиво и пеленки располагались на соседних стеллажах или что, наоборот, они находились в разных концах магазина и покупателям приходилось пересекать весь торговый зал. По сути, ни одно из этих предположений не подтвердилось. Результат анализа сочли забавным курьезом, и ни аналитики Teradata, ни менеджеры Osco Drug даже не пытались произвести какие-то действия на их основе или хотя бы оценить потенциальные их последствия.
У нас недостаточно информации, чтобы судить о том, почему этот интересный пример поиска моделей в данных так и не получил достойного продолжения. Но он наглядно свидетельствует о том, что любой этап аналитического процесса будет эффективным только в том случае, если приведет к какому-то результату. Компьютеры способны найти модели в базе данных, но только человек может сказать, есть ли в этих моделях какой-то смысл, и принять соответствующие меры (см. вставки «Компьютеры и модели: число π» и «Закон первой цифры – способ обнаружения мошенничества»).
Компьютеры и модели: число π
Число π – это отношение длины окружности к ее диаметру. π приблизительно равно 3,141592 в обычном десятичном исчислении. Многие формулы математики, инженерного дела и науки используют это значение, что и делает его самой важной математической концепцией после теоремы Пифагора
[77].
π – иррациональное число, что означает, что его значение не может быть выражено обыкновенной дробью, а последовательность знаков после запятой никогда не заканчивается и не является периодической. Однако это не значит, что человечество, начиная с древних вавилонян и до современных математиков, прекратило попытки обнаружить повторяемость в десятичных знаках π.
Конечно, появление компьютеров в XX веке привело к новым попыткам поставить рекорд, рассчитав число π до еще большего количества знаков; компьютеры полностью заменили в этом деле людей. Нынешний рекорд количества разрядов, до которых рассчитано число π, составляет пять триллионов. Дальнейшее увеличение числа разрядов зависит не столько от математических способностей человека, сколько от технических возможностей компьютеров. Тем не менее до сих пор повторяющихся групп цифр в знаках числа π не обнаружено.
Зато математики нашли множество новых применений этому замечательному числу, что говорит о важной роли креативности в аналитическом мышлении. Например, математик Дэвид Ачесон рассказывает такую историю.
Представьте себе удивление математиков, когда в середине XVII века они обнаружили появление числа π в разных областях, подчас весьма далеких от геометрии окружности. Один из самых замечательных фактов этого рода состоит в необычной связи между π и рядом нечетных чисел.
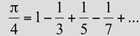
…Удивительные взаимосвязи такого рода принадлежат к явлениям, которые всегда волновали математиков»
[78].
Была обнаружена также взаимосвязь между рядом четных чисел и числом π. Более того, π появляется в уравнении «знаменитая пятерка»
[79], выведенном великим швейцарским математиком XVIII века Леонардом Эйлером. В 1988 году читатели авторитетного математического журнала признали это уравнение «самой красивой математической формулой в истории математики».
Все эти изыскания в области истории расчета и применения числа π говорят о том, что даже сейчас, когда компьютеры выполняют многие математические расчеты, креативность человеческого ума всегда найдет себе выход. Применительно к количественному анализу в сфере бизнеса и корпораций компьютеры взяли на себя подавляющее большинство статистических расчетов. Но творчеству по-прежнему есть место там, где заходит речь об использовании этих расчетов для принятия решений.
И в заключение об аналитике и креативности
Хотелось бы надеяться, что нам удалось показать читателям: аналитическое мышление и креативность не только вполне совместимы, но и тесно взаимосвязаны. Вы не сможете ни стать хорошим количественным аналитиком, ни компетентно пользоваться аналитическими данными, если не умеете подключать к делу все ваши творческие способности. Однако помните, что в манипулировании цифрами и интерпретации результатов анализа баз данных креативность должна иметь предел. Творческий подход очень важен, но правда еще важнее.
Закон первой цифры – способ обнаружения мошенничества
Профессор математики в Политехническом институте штата Джорджия Тед Хилл в начале курса дает студентам задание на дом: или подбросить монетку двести раз и записать результаты, или представить, как подбрасываешь монетку двести раз, и сфальсифицировать результаты. На следующем семинаре он просматривает отчеты о домашней работе и, к восторгу аудитории, легко обнаруживает почти всех, кто занимался фальсификациями. Как это ему удается? На основании небольшого эксперимента он знает, что в некоторый момент при длительном подбрасывании монетки начинают выходить серии из шести-семи орлов или решек подряд. «Фальсификаторы» об этом не знают и интуитивно пытаются не писать подряд слишком много одинаковых результатов, поскольку считают, что это маловероятно. Хилл с первого взгляда выявляет записи о шести-семи орлах или решках, выпавших подряд (или их отсутствие), на основе чего и делает вывод о действительно проведенном студентом эксперименте или о фальсификации его результатов. На первый взгляд, это просто небольшой фокус для привлечения внимания студентов, но на самом деле в этом есть глубокий смысл. Если в данных отсутствуют те модели и зависимости, которые вы ожидали там увидеть, логично предположить фальсификацию или мошенничество.
Мы хорошо знаем, что наша система исчисления использует цифры от 1 до 9. Поэтому можно предположить, что вероятность выбора любой из этих цифр в качестве первой значащей в числе равна 1/9. Но, как ни странно, это не так. «Закон первой цифры», называемый также законом Бенфорда, гласит, что в списке чисел, взятых из реальных баз данных, частота распределения той или иной цифры на первое место в числе подчиняется специфической закономерности: примерно в 30 процентах случаев такой цифрой будет 1, а вероятность появления на первом месте остальных цифр тем меньше, чем цифра больше
[80]. В соответствии с законом Бенфорда вероятность распределения цифр на первом месте в числе такова: