Вспомните ситуацию, когда вы с кем-то встретились и неожиданно выяснили, что у вас есть общие знакомые. Оказалось, например, что продавец местного хозяйственного магазина однажды ходил в поход по национальному парку Йосемити вместе с мужем вашей сестры, а ваша новая девушка играет в той же лиге боулинга, что и ваш босс. «Мир тесен», – говорим мы в таких случаях. Обнаруживать такие неожиданные совпадения очень забавно. Как будто на оживленной городской улице полно незнакомцев, и когда мы видим знакомое лицо, то сразу это замечаем и радуемся.
Неужели мир действительно настолько тесен? Психолог Стэнли Милгрэм и его ученик, студент Джеффри Трэверс доказали, что это действительно так. Мир даже более тесен и более связан, чем показывают нам случайные и неожиданные общие знакомства
{47}.
В 1967 г. Милгрэм и Трэверс провели знаменитое исследование. Жителям небольшого провинциального городка в штате Небраска они раздали 300 конвертов, которые нужно было передать одному биржевому маклеру из Бостона, штат Массачусетс, причем только через своих родственников и знакомых. Трэверс и Милгрэм хотели выяснить, сколько нужно времени, чтобы письмо, переходя из рук в руки, достигло адресата. В среднем потребовалось шесть «остановок», прежде чем оно добралось до дома или до офиса биржевого маклера в Массачусетсе. Другими словами, первоначальный отправитель в Небраске находился всего в шести «степенях удаленности» от адресата в Массачусетсе. Именно это исследование дало начало так называемой теории шести рукопожатий и вполне правдоподобной идее о том, что у нас есть общие знакомые с людьми, живущими на другой половине планеты.
В 2001 г. социолог Дункан Уоттс, вдохновленный открытиями Милгрэма, провел более обширное и строгое исследование международного масштаба
{48}. В нем приняли участие 18 человек в 13 странах. Среди них были работник архива из Эстонии, полицейский из Западной Австралии, профессор с севера штата Нью-Йорк. Эти люди были выбраны для того, чтобы добиться максимального разнообразия. Затем Уоттс привлек к эксперименту более 60 000 человек со всех концов Соединенных Штатов.
Им нужно было переслать электронное письмо одному из выбранных социологом людей либо своим друзьям, которые могли бы знать этого человека. Что удивительно, Уоттс проследил путь электронных писем, которые так и не дошли до адресата, и обнаружил, что Милгрэм был совершенно прав: для достижения адресата письмам в среднем понадобилось от пяти до семи пересылок.
Да, мир действительно тесен. И мы все в нем связаны друг с другом.
* * *
Исследования Милгрэма и Уоттса показывают, что планета Земля – это одна большая социальная сеть, и каждый человек в ней связан с любым другим всего лишь через шесть посредников. Мысль о том, что через наших друзей мы связаны с миллиардами людей, кажется неправдоподобной. Но для стартапа под названием «вы» она имеет весьма практические последствия. Предположим, вы решили стать врачом и хотите познакомиться с известным доктором медицины. Вы считаете, что можете сделать это через знакомых. Хорошая новость состоит в том, что вы знаете, что вас отделяет от него не больше шести других людей. Плохая – в том, что, если вы решите последовать процедурам Милгрэма или Уоттса, т. е. попросите хорошего друга отправить кому-нибудь e-mail и будете надеяться, что шесть или семь электронных адресов спустя он достигнет адресата, это не слишком надежно. Даже если письмо придет по адресу, такой способ знакомства вряд ли окажется успешным. То, что вы – друг друга друга друга друга друга, вовсе не значит, что перед вами с радостью откроют двери.
Но если бы вы видели перед собой диаграмму всей социальной сети человечества, то могли бы найти самый короткий путь от вас к вашему доктору. Сейчас таких путей становится все больше и больше. Социальные сети в Интернете превращают абстрактную идею о всеобщей взаимосвязанности в нечто реальное и практичное. По некоторым оценкам, в мире около 1 млрд профессионалов, причем 100 млн из них зарегистрировано на сайте LinkedIn, и каждую секунду появляется два новых участника. Вы можете найти в этой сети знакомых и друзей, которые смогут познакомить вас с вашим доктором, и при этом у вас будет наименьшее из возможных количество посредников. Вам не придется отправлять письмо «на деревню дедушке» в надежде, что оно достигнет адресата через шесть промежуточных «звеньев». Например, этот скриншот с сайта LinkedIn показывает количество «посредников» от одного пользователя до доктора медицины Сары Пендрелл.
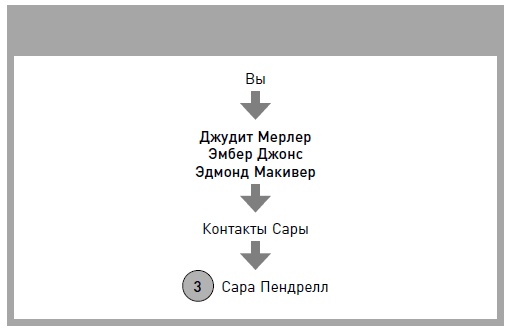
Здесь теория шести рукопожатий теряет силу. С научной точки зрения она верна, но если нам нужно познакомиться с людьми, которые могут помочь нам в профессиональной сфере, важнее всего три рукопожатия, или три степени удаленности. Три – магическое число, ведь когда мы знакомимся с контактами второго или третьего уровня, как минимум один человек в этой цепочке лично знает того, с кем мы хотим познакомиться. Это выглядит примерно так: я → Карен → Джейн → Сара.
Карен и Джейн находятся в середине этой цепочки, и обе они знакомы или с вами, или с Сарой – с двумя людьми, которые пытаются познакомиться друг с другом. Именно так возникают доверительные связи. Если добавить еще одно рукопожатие, то человек в середине цепочки не будет знать ни вас, ни Сару и поэтому никак не сможет способствовать вашему знакомству. В конце концов, зачем кому-то утруждать себя и знакомить одного незнакомца (даже если он – друг друга друга) с другим?
Итак, в нашу расширенную профессиональную сеть не входят все 7 млрд других жителей планеты, даже если они находятся на расстоянии шести рукопожатий, или степеней удаленности. Но в нее входят все те, кто находится на расстоянии двух или трех степеней, ведь с ними можно познакомиться через знакомых. Это очень большая группа. Предположим, у вас 40 друзей, и у каждого из них есть еще 35 друзей, а у каждого из этих друзей друзей есть еще 45 друзей. Если провести простые математические вычисления (40 × 35 × 45), окажется, что в целом мы можем познакомиться с 54 000 человек.
Конечно, некоторые из наших друзей знакомы друг с другом. Это немного сужает границы сети, и общее количество возможных контактов будет несколько меньше. Если зайти на страницу Network Statistics пользователя LinkedIn, где показан размер его профессиональной сети вплоть до контактов третьей степени и где отражены общие знакомые его друзей, мы увидим, что количество возможных связей все еще остается очень большим (см. диаграмму, приведенную на следующей странице).



