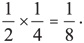Третий вид вероятности отличается от описанных выше тем, что ее не получают экспериментально и определяют не для повторяющихся событий, — скорее она выражает мнение или степень уверенности в том, что какое-то событие произойдет. Она называется субъективной вероятностью (один из ее видов — байесовская вероятность, получившая свое название по имени статистика XVIII века Томаса Байеса). Когда подруга говорит, что на 50 % уверена, что пойдет в эти выходные на вечеринку к Майклу и Джулии, она использует байесовскую вероятность, выражая некую степень уверенности в том, что так оно и будет. Каким будет уровень безработицы к следующему году? Мы не можем тут использовать частотную вероятность, потому что нельзя рассматривать безработицу следующего года как набор наблюдений, выполненных при идентичных или даже схожих обстоятельствах.
Давайте разберемся на примере. Когда ведущая прогноза погоды сообщает, что вероятность дождя завтра 30 %, мы знаем, что она не проводила экспериментов в течение нескольких идентичных в плане погодных условий дней (даже если бы такое было возможно). Цифра в 30 % выражает степень ее уверенности
(по шкале от одного до 100) в том, что будет дождь, и своей целью она ставит доведение до вашего сведения некоей информации, которая может заставить вас призадуматься, нужны ли вам будут завтра галоши и зонтик.
Если ведущая прогноза погоды — хорошо проверенный источник, то дождь будет идти в 30 % случаев, про которые она говорила, что вероятность дождя 30 %. Если дождь будет идти в 60 % случаев, то она ошиблась, и намного. Вопрос о том, насколько проверен источник, важен только в случае с субъективной вероятностью.
Кстати, давайте вернемся к вашей подруге, сказавшей, что ее шансы пойти на вечеринку равны 50 %. Многие из тех, кто не привык мыслить критически, часто допускают подобную ошибку: они полагают, что если есть два варианта, то они должны быть равновероятны. Когнитивные психологи Амос Тверски
и Дэниел Канеман
описали вечеринки и иные возможные сценарии людям, участвовавшим в эксперименте. На конкретной вечеринке, например, гостям могут сказать, что в зале присутствуют 70 % писателей и 30 % инженеров. Если вы столкнетесь с кем-то, у кого будет татуировка с портретом Шекспира, то справедливо решите, что перед вами один из пишущей братии, но если вы наткнетесь на кого-то с уравнением Максвелла
на футболке, то справедливо решите, что перед вами инженер. А что, если вы столкнетесь с человеком без опознавательных признаков — ни татуировки, ни математических формул на футболке, — какова вероятность того, что перед вами инженер? В опросах, проведенных Тверски и Канеманом, люди обычно говорили о вероятности «50 на 50», совершенно не видя разницы между двумя возможными исходами и двумя одинаково вероятными исходами
[85].
Субъективная вероятность — единственная из всех возможных, находящихся в нашем распоряжении в тех ситуациях, где нет места эксперименту и симметрии условий. Когда судья дает присяжным указание вынести вердикт, указывает ли «перевес улик» на вину ответчика, то налицо субъективная вероятность — каждый из присяжных должен самостоятельно решить, есть ли перевес, взвешивая все улики на весах собственных внутренних (возможно, не объективных) принципов и убеждений.
Когда букмекер оценивает шансы на скачках, он пользуется субъективной вероятностью — хотя послужной список лошади, здоровье и история наездника тоже могут предоставить некую информацию, тут нет естественной симметрии (это не случай классической вероятности) и тут нет никакого эксперимента (что исключает возможность частотной вероятности). Тот же принцип действует и в бейсболе или любом ином виде спорта. Букмекер может сказать, что шансы «Роялс» выиграть следующий матч равны 80 %, но это не вероятность в математическом смысле; просто таким образом он — и мы вместе с ним — использует язык, чтобы придать своим словам весомость, числовую точность. Букмекер не может повернуть стрелки часов вспять и просмотреть несколько раз один и тот же матч «Роялс», чтобы подсчитать, сколько раз они его выиграют. Он может, правда, подсчитать все математически или использовать компьютер, чтобы построить базу для оценки, но, в конце концов, его числа — всего лишь догадка, степень его уверенности в собственном предсказании. Субъективность оценок подтверждается тем, что у разных экспертов получаются разные числа
[86].
Субъективные вероятности окружают нас, при том что мы в большинстве своем их не замечаем — мы встречаемся с ними в газетах, в залах заседания совета директоров, в спортзалах. Вероятность того, что какая-нибудь страна, не отличающаяся политической чистоплотностью, в ближайшие 12 месяцев взорвет атомную бомбу, что процентная ставка возрастет в следующем году, что Италия выиграет мировой кубок или что солдаты займут определенную высоту, — всегда субъективна, это не частотная вероятность.
Это все разовые, невоспроизводимые события. И репутация экспертов и предсказателей зависит от того, насколько правильны их прогнозы.
Комбинации вероятностей
Одно из самых важных правил теории вероятностей — правило умножения. Если два события независимы друг от друга — то есть одно из них никак не влияет на исход другого, — вы получите вероятность того, что они оба произойдут, перемножив вероятности каждого. Вероятность того, что при подбрасывании монеты выпадет орел, равна одной второй (потому что существует всего два возможных варианта: орел или решка). Вероятность того, что из колоды вы вытянете червовую карту, равна одной четвертой (потому что есть четыре возможных варианта: черви, пики, трефы и бубны). Если вы подкидываете монету и вытягиваете карту, то вероятность того, что у вас получатся и орел, и черви, высчитывается с помощью умножения двух отдельных вероятностей:
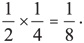
| Орел |
Черви |
Решка |
Черви |
| Орел |
Бубны |
Решка |
Бубны |
| Орел |
Трефы |
Решка |
Трефы |
| Орел |
Пики |
Решка |
Пики |
Я тут не говорю о тех редких случаях, когда вы кидаете монетку и она приземляется на ребро, или когда ее уносит чайка, пролетавшая мимо, или когда у вас в фальшивой колоде сплошь трефы.