Справедливости ради давайте предположим, что СВДС — действительно причина одной из 8543 смертей в младенчестве, как свидетельствовал доктор Мидоу, бывший экспертом в этом вопросе. Позже врач-педиатр заявил, что вероятность того, что в одной семье могут произойти два одинаковых случая — гибель ребенка в результате СВДС, — была
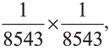 , или 1 из 73 миллионов. («Совпадение? Думаю, нет!» — мог воскликнуть обвинитель во время своей заключительной речи.) Глядя на эти подсчеты — использование правила умножения, — можно предположить, что случаи смертельного исхода независимы друг от друга, но это не обязательно так. Какие бы обстоятельства ни вызвали внезапную смерть первого ребенка миссис Кларк, нельзя забывать, что дети воспитывались в одной семье. Есть два сопутствующих фактора, связанных с СВДС: пассивное курение и сон на животе. Предположим также, что первый ребенок страдал от какого-нибудь врожденного порока. Это сильно повышает вероятность того, что нечто подобное проявится в геноме второго малыша (у детей, рожденных от одних и тех же родителей, 50 % ДНК одинаковы). Рассуждая подобным образом, можно предположить, что вероятность смерти второго ребенка по какой-нибудь подобной причине равна 50 %, — и вот миссис Кларк уже гораздо меньше похожа на убийцу.
, или 1 из 73 миллионов. («Совпадение? Думаю, нет!» — мог воскликнуть обвинитель во время своей заключительной речи.) Глядя на эти подсчеты — использование правила умножения, — можно предположить, что случаи смертельного исхода независимы друг от друга, но это не обязательно так. Какие бы обстоятельства ни вызвали внезапную смерть первого ребенка миссис Кларк, нельзя забывать, что дети воспитывались в одной семье. Есть два сопутствующих фактора, связанных с СВДС: пассивное курение и сон на животе. Предположим также, что первый ребенок страдал от какого-нибудь врожденного порока. Это сильно повышает вероятность того, что нечто подобное проявится в геноме второго малыша (у детей, рожденных от одних и тех же родителей, 50 % ДНК одинаковы). Рассуждая подобным образом, можно предположить, что вероятность смерти второго ребенка по какой-нибудь подобной причине равна 50 %, — и вот миссис Кларк уже гораздо меньше похожа на убийцу.
В конце концов ее муж нашел в архивах больницы доказательства того, что причина смерти второго малыша носила микробиологический характер. Миссис Кларк была оправдана, но к тому моменту она уже провела в тюрьме три года, отбывая наказание за преступление, которого не совершала.
Для условных вероятностей есть специальное обозначение. Вероятность того, что официант принесет вам кетчуп, при условии, что вы только что заказали гамбургер, выглядит так:
P (кетчуп | гамбургер),
где вертикальная прямая | читается как «при условии».
Обратите внимание: благодаря подобной записи исчезает необходимость в большом количестве слов, и математическая формула получается короткой.
Вероятность того, что официант принесет вам кетчуп, при условии, что вы только что заказали гамбургер и просили принести кетчуп, записывается так:
P (кетчуп | гамбургер ∧ попросил)
где ∧ читается как и.
Визуализация условных вероятностей
Относительная заболеваемость пневмонией на территории Соединенных Штатов в год составляет около 2 % — 6 миллионов человек из 324 миллионов населения страны получают этот диагноз каждый год (безусловно, сюда не входят многочисленные случаи, когда диагноз поставить не удается, а также такие ситуации, когда человек в течение года болеет пневмонией не один раз, но мы пока не об этом)
[88]. Получается, что вероятность того, что случайно выбранный для опроса человек болен пневмонией, равна приблизительно 2 %. Но мы получим более точную оценку, если будем знать хоть что-то об этом конкретном человеке. Если вы пойдете к доктору и скажете, что у вас температура, кашель и заложена грудь, то уже не будете отобраны для опроса случайно — ведь вы пришли к доктору за помощью и жалуетесь на эти симптомы. Вы можете постепенно уточнить свою уверенность в чем-либо (например, что у вас пневмония), получая все новые и новые свидетельства. Мы используем правило Байеса для вычисления условной вероятности: какова вероятность того, что у меня пневмония, при условии наличия у меня симптома x?
[89] И чем большим количеством информации вы будете обладать, тем вернее будут уточнения такого рода. Какова вероятность того, что у меня пневмония, при условии, что: 1) у меня все эти симптомы; 2) в семейном анамнезе это не первый случай; 3) я только что провел три дня рядом с человеком, больным пневмонией? Вероятность увеличивается и увеличивается.
Вы можете подсчитать вероятности, используя формулу Байеса (см. приложение), но гораздо проще и нагляднее это сделать с помощью таблички, состоящей из четырех частей и описывающей все возможные сценарии: вы заказали или не заказали гамбургер и вы получили или не получили кетчуп:
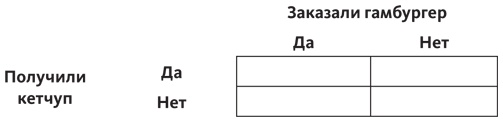
На основании экспериментов и наблюдений вы вписываете различные значения — частоту каждого события. Из 16 посетителей ресторана, обедавших в тот момент, был только один, который заказал гамбургер, и ему принесли кетчуп, а также было два случая, когда кетчуп не принесли. Эти данные идут в левый столбец:
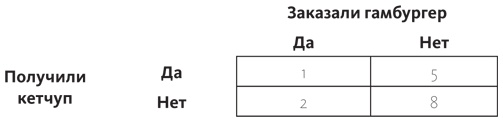
Аналогичным образом поступаем в ситуации, когда пятеро не заказывали гамбургер, но получили кетчуп, а восемь человек, которые не заказывали гамбургер, не получили кетчуп. Эти данные записываем в правый столбец:
А дальше вы просто складываете числа в строках и столбцах:
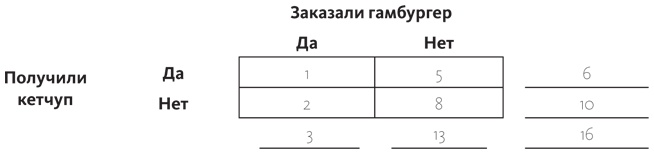
Теперь подсчет вероятностей стал делом простым. Если вы хотите узнать вероятность того, получите ли вы кетчуп при условии, что заказывали гамбургер, тогда начинайте с условия. Ему соответствует левый столбец.
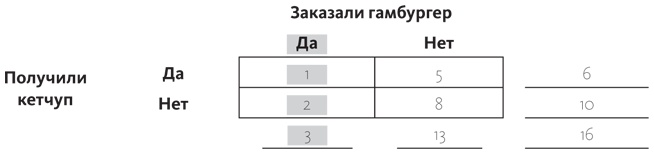
Трое посетителей заказали гамбургеры — это сумма, указанная в самом низу. Теперь попытаемся подсчитать вероятность того, что вы получите кетчуп при условии, что заказывали гамбургер. Теперь мы смотрим на клеточку «Да, получили кетчуп» в столбце «Да, заказали гамбургер», там стоит число 1. Условная вероятность P (кетчуп | гамбургер) тогда равна одной трети. И вы можете понимать это так: трое посетителей заказали гамбургер, один получил кетчуп, а двое нет. В данном виде подсчетов мы никак не задействуем правый столбец.
Мы можем использовать этот метод, когда нужно подсчитать любую условную вероятность, даже вероятность того, получите ли вы кетчуп при условии, что не заказывали гамбургер: 13 посетителей ресторана не заказывали гамбургер, пять из них при этом получили кетчуп — это значит, что вероятность равна 5/13, или около 38 %. В этом конкретном ресторане вероятность того, что вы получите кетчуп, даже не заказывая гамбургер, гораздо выше, чем если бы вы его заказывали. (А теперь давайте включим критическое мышление. Как такое могло случиться? Может, данные взяты в ситуации, когда посетители заказывали картофель фри? Или, может, все гамбургеры изначально подавались с кетчупом?)



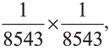 , или 1 из 73 миллионов. («Совпадение? Думаю, нет!» — мог воскликнуть обвинитель во время своей заключительной речи.) Глядя на эти подсчеты — использование правила умножения, — можно предположить, что случаи смертельного исхода независимы друг от друга, но это не обязательно так. Какие бы обстоятельства ни вызвали внезапную смерть первого ребенка миссис Кларк, нельзя забывать, что дети воспитывались в одной семье. Есть два сопутствующих фактора, связанных с СВДС: пассивное курение и сон на животе. Предположим также, что первый ребенок страдал от какого-нибудь врожденного порока. Это сильно повышает вероятность того, что нечто подобное проявится в геноме второго малыша (у детей, рожденных от одних и тех же родителей, 50 % ДНК одинаковы). Рассуждая подобным образом, можно предположить, что вероятность смерти второго ребенка по какой-нибудь подобной причине равна 50 %, — и вот миссис Кларк уже гораздо меньше похожа на убийцу.
, или 1 из 73 миллионов. («Совпадение? Думаю, нет!» — мог воскликнуть обвинитель во время своей заключительной речи.) Глядя на эти подсчеты — использование правила умножения, — можно предположить, что случаи смертельного исхода независимы друг от друга, но это не обязательно так. Какие бы обстоятельства ни вызвали внезапную смерть первого ребенка миссис Кларк, нельзя забывать, что дети воспитывались в одной семье. Есть два сопутствующих фактора, связанных с СВДС: пассивное курение и сон на животе. Предположим также, что первый ребенок страдал от какого-нибудь врожденного порока. Это сильно повышает вероятность того, что нечто подобное проявится в геноме второго малыша (у детей, рожденных от одних и тех же родителей, 50 % ДНК одинаковы). Рассуждая подобным образом, можно предположить, что вероятность смерти второго ребенка по какой-нибудь подобной причине равна 50 %, — и вот миссис Кларк уже гораздо меньше похожа на убийцу.


