Может возникнуть вопрос: какова вероятность того, что человек купил это яблоко именно в супермаркете, при условии, что у него вообще есть яблоко?
P (был в супермаркете | нашел яблоко, которое хочет купить).
Это не то же самое, как в случае, если бы вам страшно хотелось яблоко сорта медуница:
P (нашел яблоко, которое хочет купить | был в супермаркете).
Такого рода асимметрия неожиданно возникает в ситуациях, когда имеет место обман с помощью статистических данных. Если вы прочтете где-то, что гораздо больше автомобильных аварий происходит в 19:00, нежели в 7:00, то какой вывод вы сделаете?
[92] Тут даже сама формулировка утверждения весьма неоднозначна. То ли речь идет о вероятности того, что во время аварии было 19 часов, то ли о вероятности того, что в 19 часов произошла авария. Во втором случае вы смотрите на количество автомобилей на дороге в 19:00 и подсчитываете, сколько из них попадают в аварии.
Возможно, в 19:00 на дороге гораздо больше машин, чем в любое другое время суток, а также случается гораздо меньше аварий на тысячу автомобилей. Это приведет к большему количеству аварий в 19:00, чем в любое другое время суток, просто потому, что на дороге в это время находится больше транспортных средств. Сведения об уровне аварийности на дороге помогут вам определить самое безопасное время для поездки.
Есть и другой пример. Вы все, должно быть, слышали, что большинство несчастных случаев на дороге происходит на расстоянии примерно 5 километров от дома. Причина не в том, что это расстояние опасно само по себе, а в том, что в большинстве случаев люди отъезжают не очень далеко от дома, чаще всего ездят куда-то по делам в округе. Как правило, эти две интерпретации одного и того же утверждения не равносильны:
P (19:00 | авария) ≠ P (авария | 19:00).
Путаница в интерпретациях подобного рода имеет не только теоретическое значение: множество судебных дел стали результатом неправильного использования условных вероятностей, которое внесло путаницу в ранее установленные факты. Судебный эксперт может правильно подсчитать, что вероятность случайного совпадения крови с места преступления с кровью подсудимого составляет 1 %. И это совсем не то же самое, что сказать, что вероятность невиновности подсудимого равна 1 %. Видите? Интуиция снова нас подвела. Судебный эксперт говорит о вероятности совпадения группы крови при условии, что подсудимый невиновен.
P (совпадение крови | невиновность).
Говоря простым языком, о «вероятности того, что мы бы нашли совпадение, если бы подсудимый был на самом деле невиновен». Но это не та же самая цифра, которую вы хотите узнать, — какова вероятность того, что подсудимый невиновен при условии, что кровь совпала:
P (совпадение крови | невиновность) ≠ P (невиновность | совпадение крови).
Многие невиновные люди были в свое время отправлены в тюрьму по ошибке. Равно как и многие пациенты приняли неверное решение, касающееся медицинского обслуживания, исходя из ошибочного предположения:
P (положительный результат анализов | рак) = P (рак | положительный результат анализов).
И дело не только в пациентах — врачи постоянно допускают ошибки (одно исследование показало, что 90 % врачей одинаково интерпретировали две разные вероятности)
[93]. И результаты, соответственно, могут быть просто пугающими.
Один хирург, например, уговорил 90 женщин на операцию по удалению груди, так как они оказались в группе повышенного риска
[94]. Он как-то заметил, что в 93 % случаев рак молочной железы возникал у женщин, находившихся в группе повышенного риска. При условии, что у женщины диагностирован рак молочной железы, вероятность того, что она будет в этой группе, равна 93 %: P (группа повышенного риска | рак молочной железы) = 0,93. Используя четырехчастную таблицу для тысячи типичных женщин и добавляя дополнительную информацию о том, что 57 % женщин попадают в эту группу высокого риска, а также учитывая, что вероятность того, что у женщины будет рак, равна 0,8 % (как говорилось ранее), можно подсчитать условную вероятность P (рак молочной железы | группа повышенного риска). Это тот вид статистики, с которым женщине хорошо бы ознакомиться, прежде чем ложиться под нож хирурга (все цифры округлены).
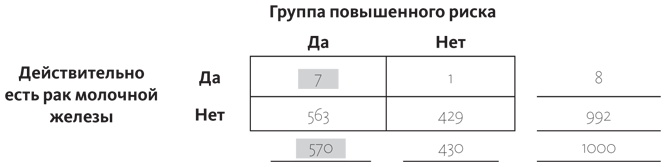
Вероятность того, что у женщины рак, при условии, что она находится в группе повышенного риска, равна не 93 %, как ошибочно полагал хирург, а только
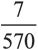 , или 1 %. Хирург переоценил риск возникновения рака примерно в 100 раз. А последствия оказались необратимыми.
, или 1 %. Хирург переоценил риск возникновения рака примерно в 100 раз. А последствия оказались необратимыми.
Составление четырехчастных таблиц может показаться странным занятием. Но составляя их, вы обращаетесь к научному, критическому мышлению и классифицируете данные визуально, чтобы облегчить себе подсчеты. А результаты последних помогают вам выразить проблему в цифрах и принять более рациональное решение, основанное на фактах.
Такие таблицы очень эффективны, и мне удивительно, что нас всех не учат составлять их в школе.
Как говорить о статистике и графиках
Большинству из нас сложно подсчитать вероятности и статистические показатели в уме, равно как и распознать тонкие закономерности, глядя на сложные таблицы, полные цифр. Мы предпочитаем живые картинки, четкие изображения и истории. Однако, принимая решение, мы придаем подобным материалам слишком большое значение по сравнению со статистическими данными. А также часто недопонимаем или неверно интерпретируем графики.




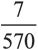 , или 1 %. Хирург переоценил риск возникновения рака примерно в 100 раз. А последствия оказались необратимыми.
, или 1 %. Хирург переоценил риск возникновения рака примерно в 100 раз. А последствия оказались необратимыми.