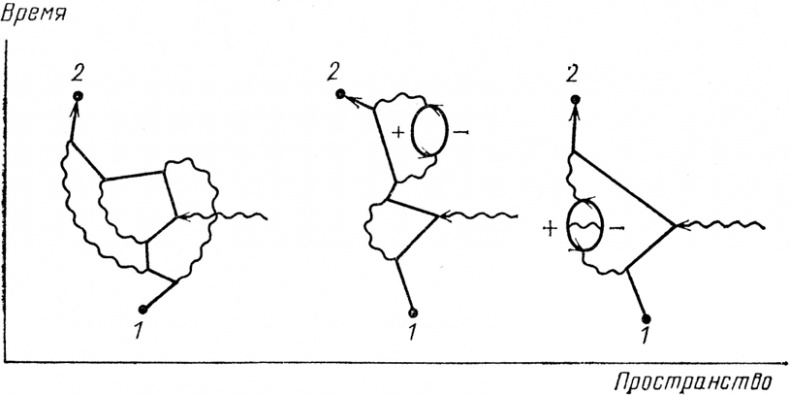
Рис. 76. И сейчас продолжаются вычисления, еще более повышающие точность теоретического значения. Следующий вклад в амплитуду, учитывающий все возможности с шестью взаимодействиями, состоит примерно из 70 диаграмм. Три из них показаны на рисунке. В 1983 г. теоретическое значение равнялось 1,00115965246 (с погрешностью около 20 в последних двух цифрах), экспериментальное – 1,00115965221 (с не-определенностью порядка 4 в последней цифре). Такая точность эквивалентна измерению расстояния от Лос-Анджелеса до Нью-Йорка (примерно 3000 миль) с точностью до толщины человеческого волоса.
Я уверен, что в ближайшие годы теоретическое и экспериментальное значения магнитного момента будут получены с точностью до еще большего числа знаков. Конечно, я не уверен, что два значения будут по-прежнему совпадать. Ничего нельзя сказать, пока не будут выполнены расчеты и эксперименты.
Итак, мы совершили полный круг и вернулись к числу, которое я выбрал в начале лекций, чтобы произвести на вас впечатление. Надеюсь, теперь вы гораздо лучше понимаете значение этого числа: по нему видно, с какой потрясающей точностью мы все время проверяем правильность этой странной теории – квантовой электродинамики.
Читая эти лекции, я получил истинное наслаждение, показывая, что столь точная теория создается ценой разрушения здравого смысла. Мы должны примириться с очень причудливыми явлениями: усилением и подавлением вероятностей, отражением света от всех частей зеркала, распространением света не по прямой и со скоростью, меньшей или большей обычной скорости света, движением электронов вспять во времени, внезапным распадом фотонов на электрон-позитронные пары, и т. д. Мы должны примириться со всем этим – чтобы осознать, какие действия Природы лежат на самом деле в основе практически всех наблюдаемых нами явлений.
Если не считать технических деталей, связанных с поляризацией, я описал вам лежащую в основе нашего понимания этих явлений концепцию. Мы рисуем амплитуду каждого из способов осуществления события, складываем эти амплитуды, в то время как в обычных условиях мы сложили бы вероятности, и умножаем амплитуды, в то время как в обычных условиях мы перемножили бы вероятности. На первых порах трудно думать обо всем на языке амплитуд из-за их абстрактности. Но человек вскоре привыкает к этому странному языку. Множество наблюдаемых нами ежедневно явлений основано всего лишь на трех основных действиях: одно описывается простой константой связи, два других – тесно связанными друг с другом функциями Р(А – В) и Е(А – В). Вот и все – и отсюда вытекают все остальные законы физики.
Однако, прежде чем закончить эту лекцию, мне хотелось бы сделать несколько дополнительных замечаний. Можно понять дух и характер квантовой электродинамики и не рассматривая технических деталей, связанных с поляризацией. Но я уверен, что вам будет как-то не по себе, если я не расскажу вам немного о том, что до сих пор опускал. Оказывается, фотоны бывают четырех видов, называемых «состояниями поляризации». Геометрически эти состояния связаны с пространственными и временным направлениями. Таким образом, имеются фотоны, поляризованные в Х-, Y-, Z- и Т-направлениях. (Возможно, вы где-нибудь слышали, что свет имеет только два состояния поляризации – например, фотон, летящий в Z-направлении, может быть поляризован только в Х– или Y-направлениях. Ну конечно, вы уже догадались: если фотон распространяется на большие расстояния и летит со скоростью света, амплитуды для Z– и Т-компонент взаимно уничтожаются. Но в атоме, когда электрон и протон обмениваются виртуальным фотоном, наиболее важна Г-компонента.)
Аналогично и электрон находится в одном из четырех состояний, которые тоже связаны с геометрией, но более тонким образом. Мы можем назвать эти состояния 1, 2, 3 и 4. Вычисление амплитуды попадания электрона из точки А пространства-времени в точку В при этом усложняется, так как мы теперь можем задавать такие вопросы: «Какова амплитуда того, что, вылетев из точки А в состоянии 2, электрон попадает в точку В в состоянии 3?» Шестнадцать возможных комбинаций – соответствующих четырем возможным начальным состояниям электрона в А и четырем возможным конечным состояниям в В – математически простым образом заключены в формуле для Е(А – В), о которой я вам уже рассказывал.
Для фотонов такой модификации не требуется. Фотон, поляризованный в Х-направлении в точке А, останется поляризованным в Х-направлении и в точке В, попав туда с амплитудой Р(А – В).
Благодаря поляризации происходит большое количество всевозможных взаимодействий. Например, мы можем спросить: «Какова амплитуда того, что электрон в состоянии 2 поглощает фотон, поляризованный в Х-направлении, и превращается в электрон в состоянии 3?» Не все возможные типы поляризованных электронов и фотонов взаимодействуют между собой, но те, что взаимодействуют, делают это с амплитудой j. (В некоторых случаях необходим еще дополнительный поворот стрелки на угол, кратный 90°.)
Существование состояний поляризации и природа взаимодействий могут быть очень изящно и красиво выведены из принципов квантовой электродинамики и двух дополнительных предположений: 1) результаты эксперимента не меняются, если экспериментальную установку повернуть на произвольный угол, и 2) они также не меняются, если установка движется в пространстве в космическом корабле с произвольной скоростью. (Это принцип относительности.) Этот изящный и общий анализ показывает, что каждая частица относится к тому или иному поляризационному классу. Так, мы говорим, что есть частицы со спином 0, спином ½, спином 1, спином 3/2, спином 2 и т. д. Частицы различных классов ведут себя по-разному. Частица со спином 0 – самая простая – имеет одну компоненту и вообще не поляризована. (Рассмотренные в этой лекции фальшивые фотон и электрон – это частицы со спином 0. Фундаментальные частицы со спином 0 до сих пор не обнаружены.) Настоящий электрон – это пример частицы со спином ½, а настоящий фотон – частицы со спином 1. Частицы со спином ½ и 1 имеют четыре компоненты. Частицы других классов имеют больше компонент; например, частицы со спином 2 имеют десять компонент.
Я сказал, что связь между относительностью и поляризацией проста и изящна, но не уверен, что смогу рассказать о ней просто и изящно! (Для этого потребовалась бы по крайней мере одна дополнительная лекция.) Хотя сложности, связанные с поляризацией, и не обязательно учитывать, чтобы понять дух и характер квантовой электродинамики, но для конкретных расчетов они, конечно, очень существенны и имеют глубокие последствия.
В этих лекциях мы сосредоточились на относительно простых взаимодействиях между электронами и фотонами на очень малых расстояниях, взаимодействиях, в которых участвует небольшое число частиц. Но я хотел бы сделать еще одно или два замечания о том, как эти взаимодействия проявляются на больших расстояниях, когда происходит обмен очень и очень большим числом фотонов. На таких больших расстояниях расчет стрелок сильно усложняется. Имеются, однако, не столь сложные для анализа ситуации. Например, бывают обстоятельства, когда амплитуда излучения фотона источником не зависит от того, излучались ли другие фотоны. Это происходит, если источник очень массивен (ядро атома) или если множество электронов будет двигаться единообразно (например, колебаться вверх и вниз в антенне радиопередатчика или вращаться по обмотке электромагнита). В этом случае излучается большое количество фотонов в совершенно одинаковых состояниях. Амплитуда поглощения фотона электроном в таких условиях не зависит от того, поглощал ли до этого фотоны этот или любой другой электрон. Поэтому все поведение и описывается просто амплитудой поглощения фотона электроном, зависящей только от положения электрона в пространстве и времени. Для описания такой ситуации физики пользуются обычными словами. Они говорят, что электрон движется во внешнем поле. Физики употребляют слово «поле» для обозначения величины, которая зависит от положения в пространстве и времени. Хороший пример поля – температура воздуха, она меняется в зависимости от того, где вы ее измеряете. С учетом поляризации у поля становится больше компонент. (А именно четыре – в соответствии с четырьмя амплитудами поглощения фотонов в разных состояниях поляризации (X, Y, Z, Т). Эти компоненты называются векторным и скалярным электромагнитными потенциалами. В классической физике из комбинаций потенциалов получаются более удобные компоненты, называемые электрическим и магнитным полями.)



