Правила построения графа легко сформулировать для случая, когда вершины соответствуют городам, а ребра — соединяющим их дорогам. Если расстояния и направления ребер правильно отражают протяженность и направленность дорог, то мы получаем простейшую географическую карту. Для графа, описывающего степень прямого взаимодействия киноактеров (рис. 15.2, б), правила построения определить гораздо сложнее. При построении такого графа непонятно, какую степень близости следует приписывать соседним вершинам графа (в нашем конкретном случае, например, паре актеров Кевин Бэкон — Эдди Альберт), не говоря уже о том, что в описываемой структуре вообще нет никакой направленности. Должен ли Джек Николсон (обладатель ЧБ = 1 за участие в фильме A Few Good Men, 1992) располагаться на том же расстоянии, что и Альберт? Проще всего расположить актеров с одинаковым значением ЧБ на одинаковом расстоянии от центра и не придавать значения направленности ребер, однако мы быстро обнаружим, что это не работает, потому что мы не сможем соединить двух актеров ребром заданной длины, так как они уже разнесены слишком далеко другими связями. Впрочем, напомню читателю, что ничто не обязывает нас рисовать граф на плоскости, так что мы вполне можем построить гораздо более удобный граф в трехмерном пространстве, где он будет напоминать дерево или строительную конструкцию. Более того, поскольку математикам, вообще говоря, безразлично, в пространстве скольких измерений они работают, то что, собственно, мешает нам построить очень красивую десятимерную веб-страницу для любителей кино и чисел Бэкона?
На самом деле в теории графов действительно не важно, каким образом будет изображена диаграмма связей различных актеров, так как при построении необходимо лишь строго следить, чтобы ребра графа точно отражали совместные съемки актеров в одном и том же фильме. Вид графа для математиков не очень важен, поскольку его важнейшие особенности полностью описываются так называемой топологией системы взаимодействий. Абсолютно разные по внешнему виду на рисунке графы могут оказаться топологически идентичными, т. е. математически одинаковыми. В некоторых случаях длины и направления ребер не играют никакой роли, поскольку они отражают только наличие связей между своими вершинами (такие графы называются реляционными). Кроме этого, существуют и так называемые пространственные графы, в которых положение вершин, а также направленность и длина ребер соответствуют реальным параметрам. Разумеется, очень часто мы сталкиваемся со схемами городов, которые, строго говоря, не являются пространственными графами. В качестве примера можно привести схему линий лондонского метрополитена (рис. 15.3), которая позднее стала образцом для многочисленных подражаний. Этот чертеж, созданный Гарри Беком в 1931 году, представляет собой отличный пример реляционного графа, но одновременно содержит и некоторые полезные признаки пространственного графа. Положения станций на схеме лишь приблизительно соответствуют их настоящему географическому расположению, расстояния между станциями приведены примерно, а направления линий метро указаны весьма неточно. Но такая схема очень полезна, поскольку позволяет легко ориентироваться в сложной системе и находить нужные пункты пересадок.
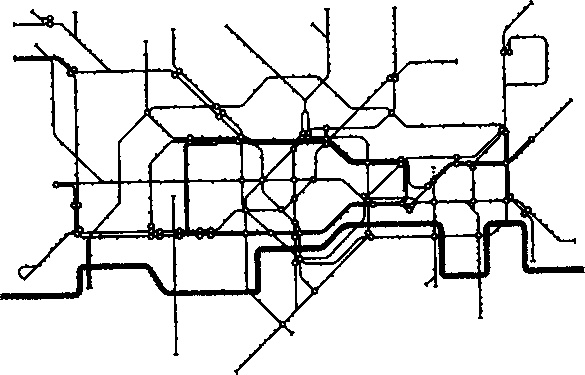
Рис. 15.3. Схема лондонского метрополитена в виде типичного реляционного графа. Положения станций (вершины) и расстояния между ними лишь приблизительно соответствуют истинным значениям. Серая линия в нижней части рисунка условно обозначает русло Темзы.
В случайных графах, изученных Эрдешем и Реньи, вершины графа соединяются случайным образом, т.е., например, при построении графа с шестью пронумерованными вершинами вы бросаете две кости и соединяете ребром две вершины, номера которых соответствуют выпавшим цифрам. Если каждая из вершин при этом оказывается связанной хотя бы с одной другой, то граф может быть назван полностью связным (рис. 15.4), и в нем можно осуществить переход из каждой вершины в любую другую (в качестве примера можно привести схему лондонского метро). В общем случае существует несколько путей, соединяющих две вершины, и возникает проблема нахождения наиболее короткого маршрута, чем обычно и озабочены пассажиры.
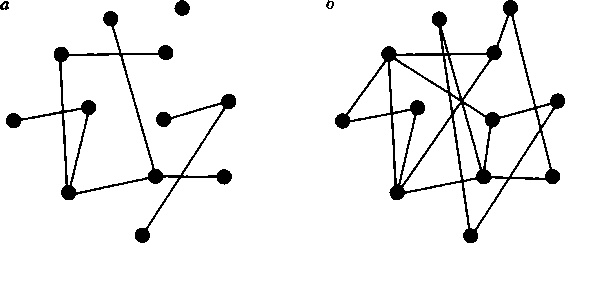
Частично связный граф Полностью связный граф
Рис. 15.4. Случайный граф считается полностью связным, если все его вершины связаны в единую сеть (б). В противном случае некоторые вершины (или даже кластеры вершин) остаются изолированными, как показано на рисунке а.
Еще в начале 1950-х годов некоторые социологи, занявшиеся приложениями теории графов (например, группа Анатоля Рапопорта в университете Чикаго), заподозрили, что графы социальных отношений и связей по своим топологическим особенностям относятся к классу случайных. Предположение оказалось не очень правильным, но очень плодотворным, поскольку случайные графы стали прекрасной моделью для понимания основополагающих структур в таких отношениях. Кроме того, Эрдеш и Реньи уже разработали очень удобный математический аппарат для исследования графов этого типа.
Свойства таких структур описываются, естественно, в терминах статистики, поскольку соединение вершин с самого начала осуществляется случайным образом. При большом числе вершин (достаточно ста) вероятность получения одинаковых графов за счет случайного совпадения соединения вершин становится пренебрежимо малой. Аналогично тому как в статистической физике нас интересовало не поведение конкретных молекул, а связанные с этим поведением усредненные характеристики газа в целом, при изучении случайных графов с большим числом вершин мы также можем ограничиться исследованием только среднего числа связей на вершинах. Естественно, что наиболее интересной и важной характеристикой является статистическое распределение вероятностей для этого числа по всей системе. Эрдеш и Реньи показали, что оно представляет собой привычную колоколообразную кривую Гаусса, пик которой соответствует среднему числу связей. Разумеется, среднее значение зависит от числа ребер графа, но для определенного случайного графа оно является вполне конкретным.
К иному (точнее сказать, противоположному) типу графов относятся регулярные решетки с одинаковыми вершинами, соединенными одинаковыми ребрами (рис. 15.5). Естественно, что математическое описание таких «упорядоченных» графов выглядит значительно проще, чем случайных. Кроме того, в этом случае не имеет смысла говорить о среднем числе ребер, так как каждая вершина, за исключением граничных или угловых, имеет одинаковое число связей (четыре для показанного на рисунке графа).
Упорядоченные и случайные графы обладают очень разными свойствами. В теории графов вообще чрезвычайно важен вопрос средней длины пути (маршрута), связывающего две случайно выбранные вершины. Эта величина называется характеристической длиной, а ее статистический смысл соответствует среднему числу пересылок пакета из Небраски в Бостон в описанном эксперименте Стэнли Мильграма. В упорядоченных графах характеристическая длина маршрута обычно довольно велика, потому что передвижение состоит из маленьких одинаковых шажков между ближайшими вершинами. В случайном графе всегда существует некоторая вероятность того, что исходная точка маршрута связана «длинной» прямой связью с вершиной, находящейся поблизости от точки назначения. Существует множество таких «коротких» путей, и соответственно характеристическая длина уменьшается по сравнению с упорядоченными графами. Более того, добавление дополнительных вершин не приводит к увеличению характеристической длины для случайных графов (в отличие от упорядоченных) и даже повышает вероятность нахождения еще более короткого маршрута.




