Означает ли сказанное, что Паутина не относится к малым мирам? Такое утверждение было бы слишком категоричным, мы лишь можем констатировать, что Паутина не принадлежит к тому классу малых миров, который придумали Строгац и Ватте. Альберт и ее коллеги пытались выявить в статистических данных одну из важных особенностей малых миров — сочетание сравнительно низкого значения среднего (характеристического) пути между вершинами с высоким коэффициентом кластеризации самих вершин. При этом они установили, что в Сети рост числа вершин сопровождается лишь очень незначительным увеличением характеристической длины (математически это сводится к тому, что характеристическая длина оказывается пропорциональной логарифму числа вершин). Исследователи показали, что граф, характеризующийся степенным законом распределения связей, действительно демонстрирует такое поведение.
Таким образом, сеть WWW все же может бьггь отнесена к малым мирам, но со специфической топологией, характеризующейся степенным законом распределения, из чего вытекает свойство безмаспггабной связности. Альберт и ее группа подсчитали, что если увеличить домен университета Нотр-Дам до размеров всей Сети, сохранив при этом его структуру, то любые две веб-страницы будут разделены в среднем 19 ссылками, при предполагаемом дальнейшем росте числа веб-страниц в 10 раз среднее число таких ссылок увеличится всего на две. То есть сама структура Сети гарантированно обеспечивает возможность достижения нужного сайта посредством всего нескольких соединений.
На первый взгляд представляется даже странным, почему эти простые закономерности не были обнаружены сразу? По мнению большинства пользователей и исследователей Сети, сложность анализа ее работы обусловлена чудовищным объемом циркулирующей в Сети бесполезной информации. Поисковые программы затрачивают массу времени, пробираясь через завалы «мусора», поскольку не существует возможности выделить только полезные ссылки. Возникает парадоксальная ситуация, при которой каждый важный документ можно действительно найти через 19 переключений, но при этом приходится просматривать массу ненужных документов, так что поразительная связность Сети автоматически снижает эффективность работы поисковых программ. Кроме того, огромные сложности для поиска информации создает непрерывное изменение размеров и параметров Сети, что заставляет любые поисковые программы тратить время на регистрацию и индексацию гигантского количества появляющихся новых страниц, а также их «привязки» к уже существующим документам. По оценкам специалистов, даже лучшие поисковые программы могут просматривать не более трети содержания Сети, а большинство программ оперируют примерно лишь с '/ш ее объема
Ладе Адамик, специалисту из исследовательского центра фирмы «Ксерокс» (Пало-Альто, Калифорния), удалось показать, что присущие Сети особенности малых миров могут быть использованы для создания более эффективных поисковых программ. Она предложила воспользоваться высокой степенью кластеризации веб-страниц, относящихся к связанным тематикам. Топология таких крупных кластеров отличается от топологии случайных графов. «Умная» поисковая машина могла бы воспользоваться этой кластеризацией для ограничения области запросов и тем самым повысить скорость и эффективность поиска. Такое осмысленное поведение представляет собой значительный шаг вперед по сравнению со случайным блужданием программ по лабиринту Сети.
Степенной закон распределения, по-видимому, является лейтмотивом Сети. Именно это распределение Адамик и ее коллега Бернардо Губерман обнаружили при анализе числа страниц на веб-сайтах. Более того, оказалось, что статистика пользователей Паутиной в 1998 году, которые прибегали при поиске информации к так называемому серфингу, тоже подчиняется показательному распределению. Серфингом называют стандартную процедуру поиска, следуя которой вы проверяете сайты по интересующей теме, а затем, пользуясь гиперссылками, двигаетесь дальше, пока не найдете нужной информации или не откажетесь от поиска.
Многие пользователи при серфинге переходят не от страницы к странице, а непосредственно от сайта к сайту. Однако группа Губермана и Адамик ограничилась анализом серфинга внутри отдельных сайтов. Их интересовала «глубина» поиска пользователей — среднее число «кликов», осуществляемых до момента выхода из сайта. Изучив весьма солидные массивы данных (поведение более 23 тысяч зарегистрированных пользователей провайдера AOL и всех посетителей веб-сайта фирмы «Ксерокс»), исследователи показали, что функция распределения вероятностей для числа «кликов» внутри сайта подчиняется степенному закону или по крайней мере очень близка к нему
[138]. Такая информация, безусловно, должна быть полезна создателям сайтов, которые могут заранее оценивать число возможных посетителей каждой веб-страницы.
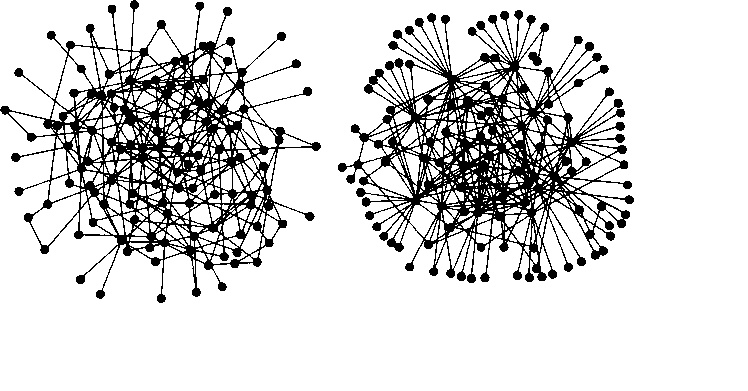
Рис. 16.3. Случайные графы (а) кажутся довольно однородными по сравнению с безмасштабными сетями (б), «присоединенными» к небольшому числу вершин с высокой связностью.
На что похожа описываемая безмасштабная сеть? Некоторое представление читатель, возможно, получит, сравнивая представленные на рис. 16.3 структуры. В случайных графах (а) большинство вершин имеет примерно одинаковое число ребер, в результате чего общая структура выглядит довольно однородной. В безмасштабной сети (б) большая часть вершин имеет лишь одну или две связи. В то же время небольшое число вершин в такой сети обладает очень большим числом соединений, что делает структуру чрезвычайно неоднородной, т. е. очень плотной в одних местах, но очень разреженной — в других. Эти высокоплотные узлы обеспечивают «короткие связи», которые делают сеть малым миром.
Интернет в целом (подобно Паутине) также обладает безмасштабной топологией, для которой распределение числа связей между узлами подчиняется степенному распределению (рис. 16.4), и именно в этом заключены его сила и фантастические возможности. Упомянутая группа Альберт, Джинга и Барабаши изучила устойчивость работы безмасштабных систем по отношению к повреждению отдельных узлов связи по сравнению с двумя другими типами сетей: случайными и сетями малых миров Строгаца и Ваттса специального типа (так называемых малых миров с доминирующей размерностью). Оба упомянутых типа сетей характеризуются тем, что вероятность образования высокосвязных узлов быстро (экспоненциально) уменьшается с ростом числа узлов и связей.





