Модель, не учитывающая индивидуальных особенностей вождения, кажется, конечно, психологически наивной и слабой, особенно учитывая разнообразие поведения людей в описанных моделях пешеходного движения, однако дело обстоит не столь просто. Вспомним, что управление машиной почти постоянно создает для водителя необычные и стрессовые ситуации. В отличие от пешехода, который почти свободен в своих движениях, водитель должен постоянно следить за дорогой, ожидая от нее разных подвохов и неожиданностей — от выскакивающих на проезжую часть детей до столкновения с другой машиной, которой управляет подвыпивший водитель. Это заставляет исследователей возвращаться к рассмотрению усредненных параметров и флуктуаций в поведении. Большинство водителей управляют машиной аккуратно и разумно, без резких изменений скорости и без столкновений с чем бы то ни было. Большинство отклонений от средних значений носит умеренный характер. Известно, например, что многие водители просто любят превышать разрешенную скорость движения на 10 миль/ч, а другие, наоборот, предпочитают езду со скоростью на 10 миль/ч ниже указанной. Лишь очень немногие предпочтут проехать от Бирмингема до Саутгемптона на третьей передаче, что когда-то проделал мой дедушка.
В дальнейшем многие ученые пытались улучшить модель Лайтхилла и сделать ее более реалистической за счет учета особенностей поведения водителей. Исследовательская группа фирмы «Дженерал моторе» в городе Уоррен (штат Мичиган) в 1950-х годах предложила первую из серии моделей «слежения» или «подражания ведущей (идущей впереди) машине». Автомобили в них считаются дискретными объектами в отличие от модели трафика как квазинепрерывного флюида, одновременно предполагается, что каждый водитель меняет скорость движения, подлаживаясь под скорость идущей впереди машины. При этом водитель может ускорять или замедлять движение машины, исходя из двух факторов: расстояния до ведущей машины и соотношения их скоростей. Водителям, движущимся со скоростью 60 миль/ч, приходится тормозить более резко, чем при скорости 20 миль/ч. В 1974 году Райнер Видеман из университета Карлсруэ предложил еще бол^е продвинутую модель, в которой каждый водитель дополнительна соблюдал ряд «психологических» правил поведения. Но чем сложнее моделі тем труднее определить, какие следствия отражают «фундаментальные* свойства дорожного движения, а какие вытекают из условий, которые мь сами заложили в модель.
Достоинством предложенной Нагелем и Шрекенбергом модели являете* ее очевидная простота, позволяющая рассматривать ее в качестве одногс из вариантов описанных клеточных автоматов. При этом автомагистралі рассматривается в виде набора клеток, каждая из которых заполнена (т. е содержит транспортное средство) или пуста, на каждом временном шаге машины перемещаются из клетки в клетку подобно фишкам в некоторы> настольных детских играх, в результате чего транспортный поток описывается последовательностью некоторых статических состояний «решетки» Подобно поведению пешеходов в модели Хелбинга каждый водитель в модели Нагеля — Шрекенберга стремится довести скорость своей машины до некоторого предпочтительного для него уровня, на свободном участке дороги каждая машина ускоряется, пока не достигнет этой скорости.
С другой стороны, водители стремятся избегать столкновений, что означает поддержание требуемой дистанции от идущего впереди автомобиля, которая, как мы все знаем, увеличивается с ростом скорости движения. Третьим компонентом модели выступает элемент случайности в поведении системы или «шум». Физический смысл введения этого компонента очевиден, поскольку ни один водитель никогда не может разгоняться или тормозить с абсолютной точностью, приходится резко жать на педаль тормоза, если водитель идущей впереди машины вдруг ни с того ни с сего начинает тормозить. Именно флуктуации скорости вызывают множество аварий, происходящих по пустяковым причинам: кто-то задумался, кто-то чуть-чуть притормозил, пытаясь рассмотреть афишу, и т. п. В сущности, к этим простым правилам и сводятся все закономерности дорожного движения в модели. Как же выглядит это движение?
Нагель и Шрекенберг в своих модельных экспериментах обнаружили два разных режима движения транспортных потоков, различающихся тем, как изменяется величина потока в зависимости от его плотности. Величина потока (ее можно назвать и пропускной способностью дороги) определяется как число машин, пересекающих контрольную точку в заданный промежуток времени (час, минута и т.д.), а плотность — как число машин на участке маршрута заданной длины (километр, миля и т.д.).
Если плотность движения возрастает, но оставляет водителям достаточно места для различных маневров, то и величина потока в целом увеличивается, так как, образно говоря, в каждом километре шоссе помещается больше машин, которые могут двигаться, не сбавляя скорости, и соответственно проходить контрольные точки в большем количестве. Этот режим движения можно назвать свободным потоком. При дальнейшем увеличении плотности машин становится столь много, что водителям приходится уже учитывать наличие соседей и соответственно тормозить, избегая столкновений, в результате чего возрастание плотности потока компенсируется снижением его общей величины. Затем при некоторой «критической» плотности характер движения существенно изменяется, а при дальнейшем повышении плотности величина потока начинает резко уменьшаться (как показано на рис. 7.1), что соответствует переходу от «свободного» режима движения к «тесному».
РИСК И СЛУЧАЙНОСТЬ
В следующей модели дорожного движения, предложенной Нагелем и Майей Пажуски в 1995 году, значение скорости, выбранное каждым водителем, продолжает затем по возможности сохраняться неизменным, что несколько напоминает систему автоматического управления скоростью (cruise-control), применяемой в некоторых автомобилях. В этих условиях процесс перехода от свободного потока к тесному как бы откладывается или даже отменяется, и после достижения критической плотности поток остается свободным, а его величина увеличивается с ростом плотности, как и раньше (рис. 7.1). Ситуация вновь выглядит так, как если бы все водители вдруг «сговорились» вести себя определенным образом, т. е. коллективно решили смириться с некоторым риском поддержания их скорости, несмотря на увеличившуюся плотность движения.
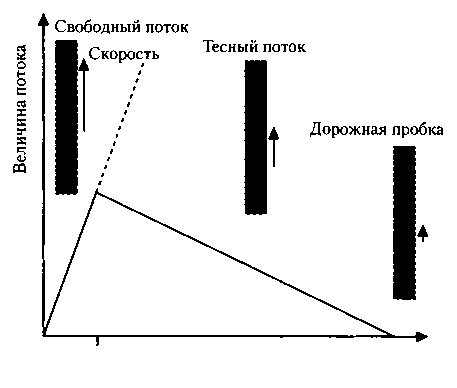
Критическая Плотность
Рис. 7.1. Зависимость величины транспортного потока от его плотности. Выделяется точка перехода от свободного потока к тесному, цосле которой повышение плотности сопровождается снижением величины потока, так как в этом режиме водители вынуждены уменьшать скорость. Выше критической точки существует также режим метастабильного «свободного» потока, показанный пунктирной линией.
Как видно из рисунка, в модели с контролем скорости критическая плотность выступает в качестве точки бифуркации, в которой становятся возможными два режима. Один из них выглядит более безопасным — все водители сбрасывают скорость, а второй несколько напоминает азартную игру, при которой все водители несутся, как прежде. До того момента, пока у кого-то из участников этой игры не сдадут нервы или не ослабнет концентрация внимания, рискованный режим позволяет обеспечить очень высокую скорость движения без столкновений. Однако это очень опасное и рискованное предприятие. Стоит хотя бы одному участнику гонки притормозить, как вынужден будет тормозить едущий следом, второй, третий, и вот в мгновение ока весь этот высокоскоростной транспортный поток превратится в тесно утрамбованное, вяло ползущее скопище. Разумеется, сохраняющие высокую скорость водители не знают, какому риску они подвергаются, точно так же как отдельные молекулы не знают, где они находятся, в газе или жидкости. Высокоскоростной режим представляется вполне осуществимым коллективным состоянием даже при плотности потока, превышающей критическую.

