53 ÷ 91 = 0,582417…
Если говорить конкретнее, ответ тут –
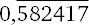, где линия над цифрами 582417 означает, что они повторяются до бесконечности. Откуда эти числа берутся? На самом деле это деление ничуть не сложнее умножения исходного двузначного числа на 11. С помощью метода, о котором мы говорили в главе 1, считаем 53 × 11 = 583. Вычитаем из этого числа единицу и получаем первую половину нашего ответа, а именно – 0,582. Вторая половина – это разность, полученная при вычитании первой половины из 999: 999 – 582 = 417. В результате получаем
.
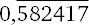Еще один пример – 78 ÷ 91. Здесь 78 × 11 = 858, то есть ответ будет начинаться с 857. Затем 999 – 857 = 142, поэтому 78 ÷ 91 =
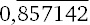. Это число нам уже встречалось в главе 1, потому что 78/91 легко упрощается до 6/7.
Метод этот работает, потому что 91 × 11 = 1001. Поэтому в первом примере
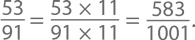А так как 1/1001 =
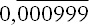, мы получаем повторяющуюся часть нашего ответа из 583 × 999 = 583 000 – 583 = 582 417.
91 = 13 × 7 дает нам отличный способ делить числа на 13, усложняя их, чтобы получить в знаменателе 91. Например, 1/13 = 7/91, а так как 7 × 11 = 077, у нас получается
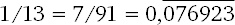
Точно так же 2/13 = 14/91 =
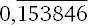, потому что 14 × 11 = 154.
Магия 10, 11, 12 и модульной арифметики
Многое из того, что мы узнали о девятке, справедливо и в отношении других чисел. Вычисляя вычет по модулю 9, мы, по сути, заменяем числа тем, что осталось от их деления на 9. Не думаю, что для вас это большая новость. Каждый из нас делает это практически каждый день – с тех самых пор, когда мы научились называть время. Допустим, часы показывают ровно 8 (утра или вечера – неважно). Сколько они будут показывать через 3 часа? А через 15 часов? А через 27? А сколько они показывали 9 часов назад? Первые числа, которые возникают в сознании – 11, 23, 35, –1, но стоит нам вспомнить, что речь идет о часах, мы понимаем, что ответ на все эти вопросы будет один и тот же – 11 часов, ведь все заданные промежутки должны считаться от 12. Математики используют для этого такого вот вида запись:
Обобщая, мы можем сказать, что a ≡ b (mod 12), где и a, и b отличаются на число, кратное 12. Соответственно, a ≡ b (mod 12), если и a, и b при делении на 12 имеют один и тот же остаток. Иными словами, для любого целого значения m мы говорим, что два числа a и b равны (сравнимы) по модулю m, что обозначается как a ≡ b (mod m) где и a, и b отличаются на число, кратное m. По сути, это значит, что
a ≡ b (mod m), если a = b + qm при целом значении q.
Самая интересное в таких сравнениях по модулю – что ведут они себя абсолютно так же, как и обычные уравнения. Вот почему мы можем пользоваться здесь модульной (модулярной) арифметикой, то есть арифметическими действиями над абсолютными значениями чисел и спокойно их складывать, вычитать и умножать. Например, если a ≡ b (mod m), а с – это любое целое число, верно будет, что
a + c ≡ b + c, а ac ≡ bc (mod m)
Итак, разнообразые сравнения можно складывать, вычитать и умножать. Например, если a ≡ b (mod m), а c ≡ d (mod m), значит,
a + c ≡ b + d, а ac ≡ bd (mod m)
Чуть более конкретно: так как 14 ≡ 2, а 17 ≡ 5 (mod 12), 14 × 17 ≡ 2 × 5 (mod 12), и это подтверждает, что 238 = 10 + (12 × 19). Следствием этого правила является то, что мы можем возводить сравнения по модулю в различные степени. Поэтому, если a ≡ b (mod m), действует следующее правило степени:
a² ≡ b² a³ ≡ b³ ··· an ≡ bn (mod m)
при положительном целом значении n.
Отступление
Почему работает модульная арифметика? Например, если a ≡ b (mod m), а c ≡ d (mod m), значит, a = b + pm, а c = d + qm для целых значений p и q. Следовательно, a + c = (b + d) + (p + q)m, а a + c ≡ b + d (mod m). Далее, применив правило FOIL, получаем
ac = (b + pm)(d + qm) = bd + (bq + pd + pqm)m
Значит, ac и bd отличаются друг от друга на число, кратное m, что приводит нас к ac ≡ bd (mod m). Умножение соответствия a ≡ b (mod m) на само себя дает a² ≡ b² (mod m); повторение этого процесса опять-таки приводит нас к правилу возведения в степень.
