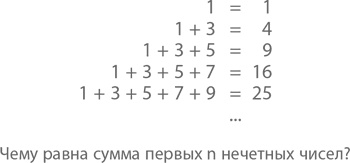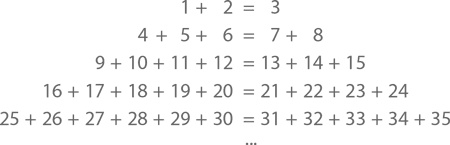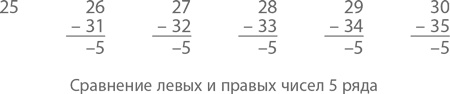Видите, закономерность, которую мы использовали для сложения первой сотни чисел, вполне применима к любому подобному ряду, сколько бы членов в него ни входило. И если вдруг нам понадобится сложить между собой все числа от 1 до 1 000 000, сделать это можно будет всего за два шага: перемножив 1 000 000 и 1 000 001 и разделив результат пополам.
Разобравшись в одной формуле, вы с легкостью разберетесь и в остальных. Например, если мы удвоим обе части последнего уравнения, получится формула суммы первых n четных чисел:
2 + 4 + 6 +… + 2n = n(n + 1)
А как насчет суммы первых нечетных, спрóсите вы? Давайте посмотрим, что говорят нам числа.
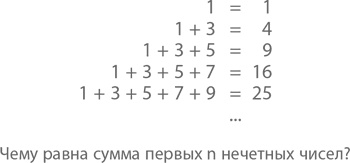
То, что справа – квадраты целых чисел. 1 × 1; 2 × 2; 3 × 3 и т. д. Сложно не заметить следующую закономерность: сумма первых n нечетных чисел равняется n × n. Или n². Но что, если это просто совпадение? Чуть позже, в главе 6, мы с вами увидим несколько путей развития этой формулы, но уже и сейчас понятно, что у такой простой закономерности должно быть не менее простое объяснение. Самое мое любимое – методом подсчета кружков: он наглядно показывает, почему числа вроде 25 называются квадратами. Но почему вдруг мы должны складывать первые 5 нечетных чисел с 5²? А просто посмотрите на квадрат размером 5 на 5:

Кружков в нем 5 × 5 = 25, это очевидно. Но давайте подсчитаем иначе. Начнем с одинокого кружка в левом верхнем углу. Его окружают 3 кружка, потом 5, потом 7 и, наконец, 9. Следовательно,
И возьми мы квадрат со сторонами n на n, его можно будет легко разбить на n-ное количество L-образных секторов, в каждом из которых будет соответственно 1, 3, 5…., (2n – 1) кружков. Это и есть формула суммы первых n нечетных чисел
1 + 3 + 5 + … + (2n – 1) = n²
Отступление
Чуть позже мы еще вернемся к методу подсчета кружков (как и к методу решения задачи двумя разными способами), и вы увидите, к каким интересным результатам он может привести в высшей математике. Но и для понимания основ он не менее полезен. Почему, например, 3 × 5 = 5 × 3? Уверен, вы никогда даже не задавались таким вопросом: просто однажды в детстве вам сказали, что порядок чисел при умножении абсолютно не важен (математики, кстати, называют это законом коммутативности). Но почему же три пакетика по пять жемчужин – это то же, что и пять пакетиков по три жемчужины? Самый простой способ объяснить этот закон – посчитать кружки в прямоугольнике размером 3 на 5. Считая ряд за рядом, мы видим 3 ряда, в каждом из них 5 кружков, то есть во всем прямоугольнике 3 × 5 кружков. С другой стороны, мы можем подсчитать столбики, а не ряды: по 3 кружка в каждом из 5 рядов, значит, всего кружков 5 × 3.
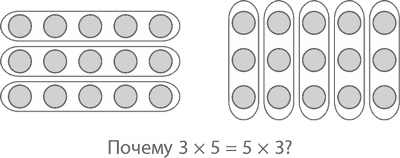
Эта закономерность может привести нас к другой, еще более красивой. Раз уж мы хотим заставить числа танцевать, почему бы не сделать это и с их квадратами?
Взгляните вот на такую пирамидку уравнений:
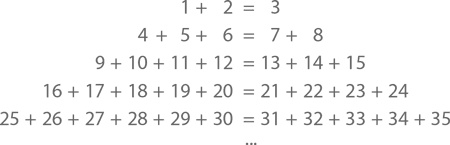
Какую закономерность вы видите? Подсчитать количество чисел в каждом ряду несложно: 3, 5, 7, 9, 11 и так далее. А дальше неожиданность: первое число каждого ряда – по крайней мере, первых 5 записанных здесь рядов – является квадратом числа. И правда: 1, 4, 9, 16, 25… Почему так получается? Возьмем пятый ряд. Сколько чисел ему предшествуют? Давайте сложим их количество: 3 + 5 + 7 + 9. Прибавим к ним еще единицу, и у нас получится первое число пятого ряда – сумма первых 5 нечетных чисел, которая, как мы уже знаем, равна 5².
А теперь просчитаем пятое уравнение, ничего к нему не добавляя. Как бы это сделал Гаусс? Если пока не обращать внимания на начальное 25, слева у нас останется 5 чисел, каждое из которых будет ровно на 5 меньше, чем соответствующее ему число справа.
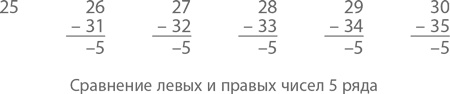
То есть сумма чисел справа будет ровно на 25 больше суммы чисел слева. Но это без учета 25, которые стоят в начале. А с ними у нас получается именно тот результат, который обещан нам знаком равенства. Следуя той же логике и призвав на помощь алгебру, мы докажем, что этот ряд можно продолжать бесконечно.
Отступление
А теперь – специально для тех, кто хотел немного алгебры. Ряду n предшествует количество чисел, равное 3 + 5 + 7 +… + (2n – 1) = n² – 1, поэтому левая сторона нашего уравнения должна начинаться с числа n², за которым следует n последовательных чисел, от n² + 1 до n² + n. Справа – n последовательных чисел, начиная с n² + n + 1, заканчивая n² + 2n. Если мы временно «забудем» про число n² слева, то увидим, что каждое из n чисел справа на n больше, чем соответствующее ему последовательное число слева. Разница при этом составляет n × n, то есть n². Закономерность эта компенсируется начальным n² слева, поэтому-то левая и правая части и равны.
Перейдем к другой закономерности. Как мы уже видели, из нечетных чисел можно составлять квадраты. А теперь посмотрим, что произойдет, если собрать их в один большой треугольник – вроде того, что изображен чуть ниже.
Так отлично видно, что 3 + 5 = 8, а 7 + 9 + 11 = 27, а 13 + 15 + 17 + 19 = 64. Что общего у 1, 8, 27 и 64? Да это же полные кубы чисел! Например, если сложить между собой пять чисел пятого ряда, мы получим:

21 + 23 + 25 + 27 + 29 = 125 = 5 × 5 × 5 = 5³
Логика вроде бы подсказывает, что сумма чисел в ряду n будет равна n³. Но насколько верным будет этот вывод? Не простое ли это совпадение? Чтобы лучше понять эту закономерность, посмотрим на числа в середине 1, 3 и 5 рядов. Что мы видим? 1, 9 и 25. То есть квадраты. В середине 2 и 4 рядов чисел нет, но по сторонам центра 2 ряда видим числа 3 и 5, среднее арифметическое которых – 4, а по сторонам центра 4 ряда – 15 и 17 со средним арифметическим 16. Давайте подумаем, как эту закономерность можно использовать.