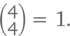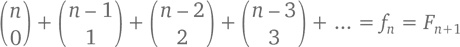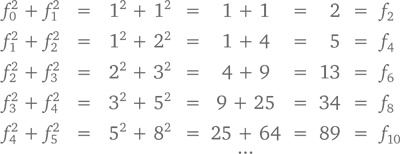Вопрос: Сколько существует возможных комбинаций единиц и двоек, дающих в сумме 8?
Ответ номер один: Судя по тому, о чем мы говорили чуть выше, – f8 = F9.
Ответ номер два: Представим себе эту проблему как 5 частных задач, в основе каждой из которых лежит количество двоек в комбинации. Сколько комбинаций обойдется вообще без двоек? Разумеется, только одна – 11111111. И поэтому совсем не случайно, что
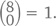
С одной двойкой? Уже семь: 2111111, 1211111, 1121111, 1112111, 1111211, 1111121, 1111112. Каждая из них состоит из семи цифр, и, смещая двойку шаг за шагом, получаем
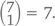
С двумя двойками (скажем, 221111)? Не будем перечислять их все, просто отметим, что любая из них будет состоять из двух двоек и четырех единиц, то есть всего из шести цифр, что дает нам
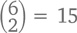 возможных местоположений двоек. По той же логике комбинации с тремя двойками будут включать в себя две единицы и состоять из 5 цифр, а общее их количество будет равняться
возможных местоположений двоек. По той же логике комбинации с тремя двойками будут включать в себя две единицы и состоять из 5 цифр, а общее их количество будет равняться
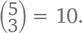 И наконец, из четырех двоек у нас получится всего одна комбинация (а именно 2222), потому что
И наконец, из четырех двоек у нас получится всего одна комбинация (а именно 2222), потому что
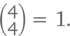
Оба ответа отлично проясняют всю ситуацию. И заодно объясняют, почему сумма чисел n-ной диагонали треугольника Паскаля равна одному из чисел последовательности Фибоначчи. То есть при n ≥ 0 сложение чисел диагонали n (вплоть до того момента, пока через n/2 шагов мы не выйдем за границы треугольника) дает нам
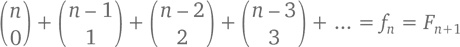
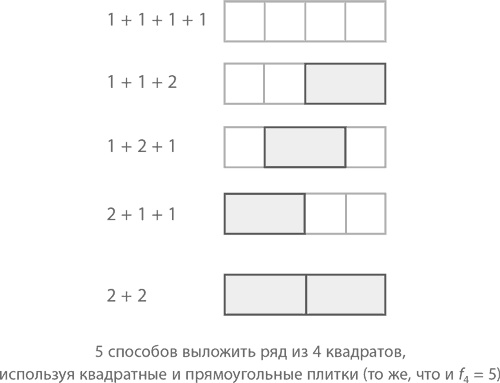
К тому же можно прийти, представив последовательность Фибоначчи в виде плиток черепицы. Тогда f4 = 5 означает 5 способов выложить один ряд (условно состоящий из 4 квадратов) одинарными (в виде квадратов) и двойными (в виде прямоугольников) плитками. То есть 1 + 1 + 2 будет выглядеть как «квадрат – квадрат – прямоугольник».
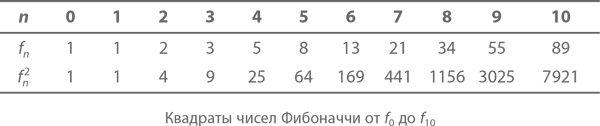
Такую визуализацию можно использовать, чтобы понять другие закономерности, основанные на числах Фибоначчи. Давайте посмотрим, что произойдет, если возвести числа Фибоначчи в квадрат.
В том, что, сложив два соседних числа последовательности Фибоначчи, мы получим следующее за ними, ничего нового для нас нет (в конце концов, именно так и появилась эта последовательность). А теперь посмотрите на числа Фибоначчи, возведенные в квадрат и сложенные между собой:
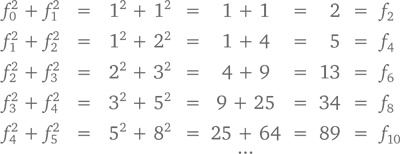
Попробуем объяснить эту закономерность с точки зрения счета. Последнее уравнение утверждает, что
Почему? Ответим на простой вопрос.
Вопрос: Сколькими способами можно выложить из квадратов и прямоугольников ряд длиной в 10 квадратов?
Ответ 1: Естественно, f10. Вот один из вариантов – визуализация суммы 2 + 1 + 1 + 2 + 1 + 2 + 1.

То есть разрывы между плитками у нас будут после 2, 3, 4, 6, 7, 9 и 10 квадратов (попросту – везде, кроме центральной оси прямоугольников, в нашем примере – это после 1, 5 и 8 квадратов).
Ответ 2: Решим две задачи: сначала посчитаем варианты кладки, в которых будет разрыв после 5 квадрата (то есть ряд можно разделить пополам), потом те, где разрыва в этом месте не будет (и ряд будет разделяться на две неравные части). Начнем с первого. Левую часть можно выложить f5 = 8 способами. Обе части равны, значит, и правую можно выложить f5 = 8 способами. Согласно закону произведения (см. главу 4), мы можем представить общую сумму способов как f5² = 8², как показано ниже:
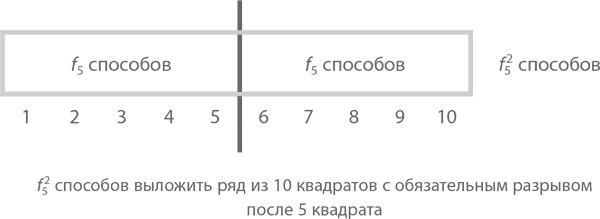
Теперь посчитаем те варианты, в которых разрыва в центре нет, зато мы точно знаем, что 5 и 6 квадраты закрыты прямоугольником (как нарисовано ниже). В таком случае части ряда как слева, так и справа от центрального прямоугольника можно выложить f4 = 5 способами, значит, всего получается f4² = 5². Сводим вместе оба варианта и получаем, что f10 = f5² + f4², что и требовалось.
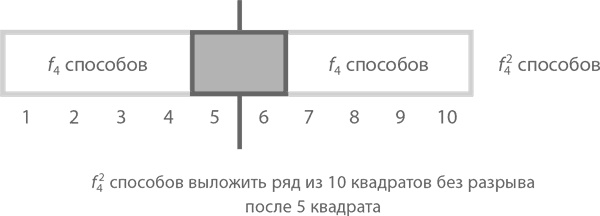
На уровне обобщений же трюк с разделением панелей длиной 2n квадратов на два типа в зависимости от того, есть ли у них по центру разрыв или нет, приводит нас к очень красивой закономерности –
f2n = fn2 + f²n–1
Отступление
Возьмем только что рассмотренную закономерность и попробуем использовать ее в похожих примерах. Скажем, сколько будет способов выложить плиткой ряд протяженностью m + n? Сначала – те варианты кладки, в которых будет разрыв после квадрата m. Левую часть можно выложить fm способами, правую – fn способами, то есть всего их fm fn. Теперь – варианты кладки без разрыва после квадрата m. Прямоугольник тогда покрывает квадраты m и m + 1, остальные же можно выложить fm–1 fn–1 способами. В итоге у нас получается весьма полезная формула при m, n ≥ 0.

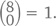
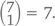
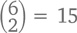 возможных местоположений двоек. По той же логике комбинации с тремя двойками будут включать в себя две единицы и состоять из 5 цифр, а общее их количество будет равняться
возможных местоположений двоек. По той же логике комбинации с тремя двойками будут включать в себя две единицы и состоять из 5 цифр, а общее их количество будет равняться
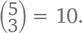 И наконец, из четырех двоек у нас получится всего одна комбинация (а именно 2222), потому что
И наконец, из четырех двоек у нас получится всего одна комбинация (а именно 2222), потому что