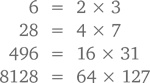В интервале от 1 до 100 насчитывается 25 простых чисел, от 101 до 200 – 21, от 201 до 300 – 16. И тенденция эта сохраняется: чем дальше мы продвигается, тем реже встречаются простые величины (без всякой, впрочем, системы: в промежутке от 301 до 400 их снова 16, а в промежутке от 401 до 500 – 17) – а от 1 000 000 до 1 000 100 мы их найдем всего лишь 6. Объяснение этому вполне очевидно: чем больше число, тем больше потенциальных делителей у него будет.
Давайте попробуем доказать, что есть такие сотни чисел, в которых простых чисел не будет вовсе (и не только сотни – тысячи, миллионы, сколько угодно). Для этого будет достаточно подобрать 99 последовательно идущих друг за другом составных чисел:
100! + 2, 100! + 3, 100! + 4…., 100! + 100
Так как 100! = 100 × 99 × 98 ×… × 3 × 2 × 1, его можно разделить на все числа от 2 до 100. Возьмем теперь 100! + 53. Так как 53 – делитель 100! оно должно являться делителем и 100! + 53. Та же логика подсказывает, что при 2 ≤ k ≤ 100 100! + k должно быть кратным k, а следовательно, составным.
Отступление
Обратите внимание, что мы пропустили 100! + 1. Впрочем, ничто не мешает нам взять и его. На этот счет существует очень интересная теорема – теорема Вильсона, которая утверждает, что число n является простым тогда и только тогда, когда (n – 1)! + 1 делится на n без остатка. Применим ее к нескольким малым величинам: 1! + 1 = 2, что кратно 2; 2! + 1 = 3, что кратно 3; 3! + 1 = 7, что не кратно 4; 4! + 1 = 25, что кратно 5; 5! + 1 = 121, что не кратно 6; 6! + 1 = 721, что кратно 7; и т. д. Следовательно, поскольку число 101 – простое, согласно теореме Вильсона, 100! + 1 является кратным 101 и потому составным. Значит, промежуток от 100! до 100! + 100 содержит в себе непрерывную последовательность, состоящую из 101 составного числа.
Итак, чем больше числа, тем меньше среди них попадается простых. Вполне логично было бы предположить, что рано или поздно они перестают попадаться вовсе. Но только не в этом случае, как больше 2000 лет назад предупредил нас Евклид. Дерзнем не поверить великому греку на слово и докажем это сами.
Теорема: Количество простых чисел бесконечно.
Доказательство: Предположим обратное – что количество простых чисел конечно. Значит, существует некое наибольшее простое число. Обозначим его литерой P. Возьмем число P! + 1. Так как P! делится на все числа в промежутке от 2 до P, ни одно из них нельзя разделить на P! + 1 без остатка. Следовательно, простой множитель P! + 1 будет больше P, что противоречит нашему условию, что P есть наибольшее простое число.◻
И хотя мы никогда не найдем наибольшее простое число, математики и специалисты по вычислительной технике не оставляют попыток зайти в этих поисках все дальше и дальше в бесконечность числового ряда. Самым большим известным науке простым числом на настоящий момент является число, состоящее из 17 425 170 цифр. Чтобы его записать, потребуется примерно сотня томов – каждый объемом не меньше книги, которую вы сейчас держите в руках. Но можно уместить и в одну строку –
А все благодаря существованию удивительно действенных методов, которые позволяют легко определить, являются ли числа вида 2n – 1 или 2n + 1 простыми.
Отступление
Великий Пьер де Ферма доказал, что если p – это нечетное простое число, то число 2p–1 – 1 должно быть кратно p. Проверим это на примере нескольких первых нечетных простых чисел. Для 3, 5, 7 и 11 мы видим, что 2² – 1 = 3, что кратно 3; 24 – 1 = 15, что кратно 5; 26 – 1 = 63, что кратно 7; 210 – 1 = 1023, что кратно 11. Что касается составных чисел, совершенно ясно, что при четном значении n 2n–1 – 1 будет нечетным, а потому кратным n быть никак не может. Составные же нечетные, вроде 9, 15 или 21, дают нам 28 – 1 = 255, что не кратно 9; 214 – 1 = 16 383, что не кратно 15; 220 – 1 = 1 048 575, что не кратно 21 (да хотя бы и 3).
Следствием теоремы Ферма является то, что, если при наибольшем значении числа N 2N–1 – 1 не кратно N, мы можем со стопроцентной уверенностью утверждать, что N не может быть простым, при этом нам даже необязательно знать его множители! Тем не менее это не совсем так: существуют такие составные числа, которые ведут себя абсолютно как простые (и по этой причине называются псевдопростыми). Самый простой пример – 341 = 11 × 31: 2340 – 1 вполне себе кратно 341. И хотя встречаются такие числа крайне редко, их количество все же бесконечно, а для их определения придуманы специальные методы.
Простые числа активно используются в повседневной жизни – в частности, в вычислительной технике при создании алгоритмов кодирования (на них, например, построена система шифрования с открытым ключом, которая используется при совершении финансовых операций онлайн). В большинстве своем они построены на методах быстрого определения того, является ли то или иное число простым. Жаль только, что нет настолько же эффективных способов быстрого разложения на множители по-настоящему огромных чисел. Так, если я перемножу два случайных тысячезначных числа и скажу вам двухтысячезначный ответ, вы никогда в жизни не сможете найти составляющие его простые величины – ни сами, ни с помощью компьютера (конечно, если этот компьютер не квантовый – а такие собирать пока еще попросту не научились). Зато представляете, насколько надежны коды (вроде алгоритма RSA
[17]), в основе которых лежит эта неспособность?
Интерес человечества к простым числам стар, как само человечество. Древние греки называли число, равное сумме его делителей (естественно, за исключением самого этого числа), совершенным. Среди них, например, число 6, сумма делителей которого – 1, 2 и 3 – равна 6. Или 28, получающееся из сложения 1, 2, 4, 7 и 14. Дальше следуют 496 и 8128. Интересно, складываются они в какую-нибудь закономерность? Попробуем разложить их на множители:
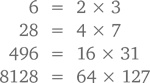
Видите закономерность? Первое число – это степень основания 2. Второе – на единицу меньше, чем удвоенная степень основания 2; и при этом оно простое (поэтому здесь и нет 8 × 15 или, скажем, 32 × 63: ведь 15 и 63 простыми числами не являются). Закономерность эту можно сформулировать в виде теоремы.
Теорема: Если число 2n – 1 является простым, число 2n–1 × (2n – 1) будет совершенным.