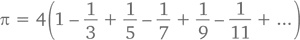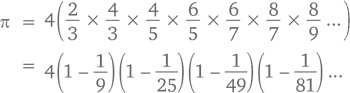Лично мне больше всего нравится последняя. И не только потому, что она совпадает с π в 6 из всего множества знаков после запятой, но и потому, что использует первые три нечетных числа (причем по два раза и по порядку!): две единицы, две тройки и две пятерки.
Не знаю, как у вас, но у меня руки прямо-таки чешутся найти такую простую дробь, которая полностью бы соответствовала π, – с целыми величинами в роли как числителя, так и знаменателя (чтобы не было соблазна сжульничать и написать что-нибудь вроде
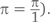 Но в 1768 году немец Иоганн Генрих Ламберт доказал, что любые подобные поиски заранее обречены на провал, потому что число π есть величина иррациональная.
Но в 1768 году немец Иоганн Генрих Ламберт доказал, что любые подобные поиски заранее обречены на провал, потому что число π есть величина иррациональная.
Может быть, тогда можно представить его в виде квадратов или кубов простых чисел? Ведь есть же, например, √10 = 3,162…, что очень близко к желаемому результату. Однако в 1882 году другой немецкий математик, Фердинанд фон Линдеман, доказал, что π есть величина не просто иррациональная, но трансцендентная – такая, которая не является корнем ни одного многочлена с целым коэффициентом (число √2, например, будет иррациональным, но не трансцендентным, потому что представляет собой корень многочлена x² – 2).
Впрочем, представить π в простом дробном виде все же можно. Правда, это будет не одна дробь, а сумма или произведение нескольких – вплоть до бесконечности. В главе 12, например, мы увидим, что
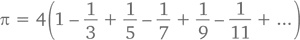
Формула эта настолько прекрасна, даже обворожительна, что даже не хочется верить, что π с ее помощью вычислять придется очень и очень долго: после трехсотого элемента мы будем настолько же далеко от заветного 3,14…, насколько далеко от него банальное 22/7.
А вот еще одна недурная попытка, называемая формулой Уоллиса, – представление π в виде бесконечного (то есть считать придется все равно очень долго, пусть и не настолько, насколько в случае с суммой) произведения:
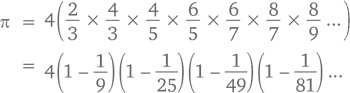
Запомним π (а заодно и τ) во славу его!
Число π продолжает будоражить самые светлые умы и по сей день. С его помощью даже испытывают суперкомпьютеры на быстродействие и точность вычислений – можете себе представить, насколько оно просчитано «в глубину» – на триллионы цифр после запятой. Практического толку от такой точности, конечно, чуть: даже 40 знаков π достаточно, чтобы просчитать размеры пределов наблюдаемой Вселенной с точностью до радиуса одного атома водорода!
Число π – уже почти религия. У ее последователей даже праздник свой есть, он так и называется – День числа π – и празднуется 14 марта (3-й месяц, 14-й день) – в день рождения Альберта Эйнштейна. В честь праздника энтузиасты пекут пироги на математическую тему, надевают маски автора теории относительности и участвуют в конкурсах по воспроизведении наизусть как можно большего количества знаков после тройки и запятой. Рядовой участник такого конкурса помнит, как правило, от нескольких их десятков до нескольких сотен. Рекорд же принадлежит китайскому студенту Чао Лю, добравшемуся в 2005 году до 67 891 цифры! В Книге рекордов Гиннесса говорится, что на одно лишь оглашение числа у него ушло больше 24 часов, на запоминание – около четырех лет.
Вот первые 100 цифр π:
π = 3,141592653589793238462643383279502884197169399375
105820974944592307816406286208998628034825342117067…
Как только люди не пытались сохранить их в памяти! Один из самых популярных методов – составлять предложения-«запоминалки», в которых количество букв в каждом слове равно числовому значению соответствующей цифры. Пожалуй, наиболее известные из них – английские «How I wish I could calculate pi»
[23] (охватывает 7 знаков: 3,141592) и «How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics»
[24] (а здесь этих знаков уже 15).
Самая, пожалуй, забавная из них – пародия на знаменитого «Ворона» Эдгара Аллана По, созданная в 1995 году Майком Китом
[25] для первых 740 знаков числа π. Одна лишь первая строчка (вместе с именем автора и заглавием) покрывает 42 цифры. Слово из 10 букв считается цифрой 0.
Позже Кит переработал и дополнил свой опус – так родилась его знаменитая «Кадеическая каденция»
[26] (Cadaeic Cadenza) – уникальное произведение, в котором «зашифровано» 3835 цифр числа π. (Слово «Cadaeic» – тоже своего рода «шифр» π, в основе которого лежат порядковые номера букв латинского алфавита: C – 3, A – 1, D – 4, A – 1, E – 5, I – 9, C – 3. Сейчас оно стало термином, обозначающим жанр подобного рода поэтических экспериментов.) Кроме «Ворона», в нее входят пародии на другие известные стихи, вроде «Бармаглота» Льюиса Кэрролла
[27]. Самым грандиозным трудом Кита, без сомнений, является «Во сне: грезы о первом десятке тысяч цифр числа π»
У этого метода есть один существенный недостаток: даже выучив наизусть все эти длинные предложения, стихотворения и целые рассказы, вы вряд ли сможете моментально определить количество букв в произносимых вами словах.
Мне больше по душе другой «шифр» – буквенный, в котором каждая цифра представлена одной или несколькими родственными согласными
[28]:



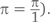 Но в 1768 году немец Иоганн Генрих Ламберт доказал, что любые подобные поиски заранее обречены на провал, потому что число π есть величина иррациональная.
Но в 1768 году немец Иоганн Генрих Ламберт доказал, что любые подобные поиски заранее обречены на провал, потому что число π есть величина иррациональная.