А что со сложением? Чему, например, равна сумма 3 и 4i? Очевидно, что 3 + 4i, и дальше с этим ничего сделать нельзя (равно как и ничего нельзя сделать с 1 +√3). Числа, образованные по модели a + bi (где a и b суть действительные величины), называются комплексными. Получается, что любая величина, будь она действительной (при b = 0) или мнимой (при a = 0), есть, по своей сути, особая форма комплексного числа. То есть действительное π и мнимое 7i будут также комплексными.
Давайте попробуем разобраться в этом с помощью нескольких конкретных примеров. Начнем со сложения и вычитания:
(3 + 4i) + (2 + 5i) = 5 + 9i
(3 + 4i) – (2 + 5i) = 1 – i
Для умножения применим алгебраический метод FOIL, описанный в главе 2:
(3 + 4i)(2 + 5i) = 6 + 15i + 8i + 20i² = 6 – 20 + (15 + 8)i = –14 + 23i
Для комплексного числа каждый квадратный многочлен ax² + bx + c будет иметь два корня (или же один, но повторяющийся). Согласно формуле корней квадратного уравнения, многочлен будет равен 0 всякий раз, когда
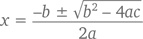
Помните, в главе 2 мы с вами говорили о том, что нельзя извлечь квадратный корень из отрицательной величины? Но ведь никакие квадратные корни отрицательных величин нам и не нужны. Смотрите сами: уравнение x² + 2x + 5, например, имеет корни
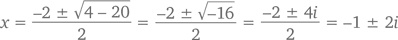
Кстати, формула корней квадратного уравнения будет верна даже при комплексных значениях a, b или c.
В любом квадратном многочлене мы можем найти как минимум один корень, пусть и комплексный. На этот счет есть своя теорема.
Теорема (основная теорема алгебры): Любой многочлен p(x), возводимый в первую или бо́льшую степень, имеет корень z при p(z) = 0.
Обратите внимание, что многочлен первой степени, вроде 3x – 6, может быть представлен как 3(x – 2), где 2 есть единственный корень 3x – 6. Обобщая, можно сказать, что при a ≠ 0 многочлен ax – b можно представить в виде a(x – (b/a)), где b/a будет являться корнем ax – b.
То же происходит и с многочленами второй степени: разложив ax² + bx + c до a(x – z1)(x – z2), мы получаем его корни – z1 и z2 (они вполне могут оказаться комплексными величинами, равно как и одной и той же величиной). И так можно продолжать до бесконечности – с любым многочленом любой степени.
Сопутствующая теорема: Любой многочлен степени n ≥ 1 может быть разложен на n составляющих. А именно: если p(x) есть многочлен n-ной степени, в котором главный член a ≠ 0, должно существовать n чисел z1, z2…., zn (которые вполне могут оказаться комплексными величинами, равно как и одной и той же величиной), соответствующих p(x) = a(x – z1)(x – z2)… (x – zn). Величины zi являются корнями многочлена при p(zi) = 0.
Теорема эта означает, что любой многочлен степени n ≥ 1 будет иметь как минимум один и как максимум n различных корней.
Например, x4 – 16 есть многочлен четвертой степени. Следовательно, его можно разложить как
x4 – 16 = (x2 – 4)(x2 + 4) = (x –2)(x + 2)(x – 2i)(x + 2i)
из чего очень хорошо видно, что у него будет четыре различных корня: 2, –2, 2i, – 2i.
А вот многочлен третьей степени 3x³ +9x² –12 раскладывается так:
3x³ + 9x² – 12 = 3(x² + 4x + 4)(x – 1) = 3(x + 2)²(x – 1)
то есть имеет только два различных корня: –2 и 1.
Геометрия комплексных чисел
Комплексные числа можно представить в виде комплексной же плоскости. Выглядит она так же, как и алгебраическая система координат (x, y), только вместо оси y мы чертим некую мнимую ось, на которой расположены числа 0, ±i, ±2i и так далее. Вот как будут выглядеть на этой плоскости некоторые комплексные величины:
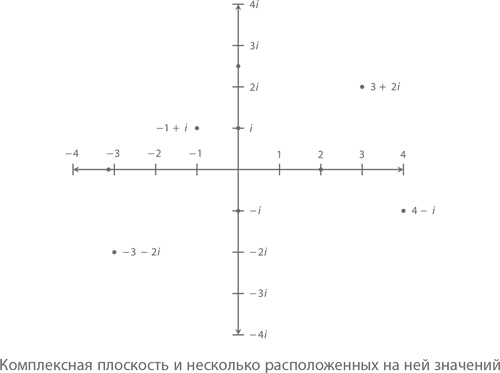
Только что мы выяснили, насколько легко складывать, вычитать и умножать числовые выражения комплексных величин. С их геометрическими представлениями работать ничуть не сложнее: достаточно просто взглянуть на соответствующие точки.
Возьмем, к примеру, сложение:
(3 – 2i) + (–1 + i) = 2 + 3i
Посмотрите на график ниже: точки 0, 3 + 2i, 2 + 3i и –1 + i образуют параллелограмм.
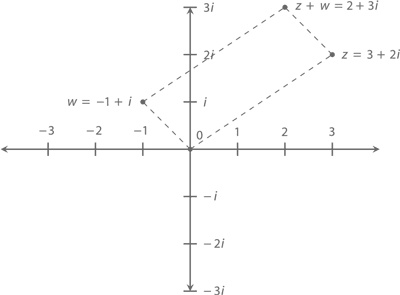
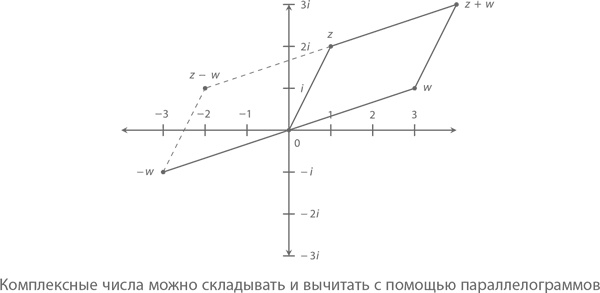
Вы удивитесь, но его вполне достаточно, чтобы сложить комплексные числа z и w.
Для вычитания z – w возьмем третью точку – w, расположенную симметрично напротив w. А теперь просто сложим z и – w, как показано на графике:
Для умножения и деления нам понадобится измерить комплексные величины. Модулем (или длиной) любого комплексного числа считается длина отрезка от начала координат 0 до точки, соответствующей искомому числу. То есть модуль числа z (обозначается как |z|) есть расстояние от 0 до точки z. Если z = a + bi, тогда, согласно теореме Пифагора, модуль z будет равен

