из чего следует
Например, так как 10² = 100, lg 100 будет равен 2. Вот очень полезная таблица логарифмов:

Одной из причин популярности логарифмов является их уникальная способность преобразовывать огромные значения в малые, куда более удобоваримые для человеческого ума. Логарифмы, в частности, используются при измерении и подсчете магнитуды землетрясения по шкале от 1 до 10 (да-да, это я о знаменитой шкале Рихтера), громкости звука (в децибелах), кислотности химических растворов (pH) и даже рейтинга посещаемости интернет-страниц (в алгоритме PageRank, придуманном корпорацией Google).
Что собой представляет lg 512? Любой профессиональный калькулятор (равно как и большинство поисковых систем в Интернете) скажет вам, что log 512 = 2,709…. Вполне похоже на правду: 512 находится между 10² и 10³, а значит, его логарифм должен быть больше 2, но меньше 3.
Логарифмы были изобретены для того, чтобы преобразовывать умножение в более простое сложение. Основано это на одной любопытной теореме.
Теорема: Для любых положительных значений x и y
Другими словами, логарифм произведения равен сумме логарифмов.
Доказательство: Согласно правилам действий со степенями,
10lg x + lg y = 10lg x 10lg y = xy = 10lg xy
Следовательно, возведение 10 в степень lg x + lg y дает xy, что и требовалось доказать.◻
Не менее полезно следующее правило.
Теорема: Для любого положительного значения x и любого целого значения n
Доказательство: Согласно правилам действий со степенями, abc = (ab)c. Следовательно,
10n lg x = (10lg x)n = xn
то есть логарифм xn равен n lg x.◻
Десятичный логарифм – штука вполне себе обычная, насколько вообще обычным может быть нечто столь активно использующееся в таких важных областях науки, как химия, физика или геология (справедливости ради все же следует упомянуть, что в информатике и дискретной математике предпочтение отдается логарифму с основанием 2). В целом же для любого значения b > 0 логарифм по основанию b logb определяется согласно следующему правилу
Так, log2 32 = 5, потому что 25 = 32. А все уже рассмотренные нами свойства логарифмов соответствуют любому значению b. Так, например,
blogb x = x
logb xy = logb x + logb y
logb xn = n logb x
В большинстве разделов математики, физики и техники самым полезным считается логарифм по основанию b = e. Он называется натуральным и даже имеет свое специальное обозначение – ln x. То есть
Или же, для всех действительных значений x,
Ваш калькулятор, например, может за долю секунды подсчитать, что ln 5 = 1,609…, однако это нам уже хорошо известно по тому, что e1,609 ≈ 5. Подробнее же о функциях натурального логарифма мы поговорим в главе 11.
Отступление
Большинство профессиональных калькуляторов способно считать как натуральные, так и десятичные логарифмы. И лишь очень немногие ориентированы на другие значения b. Впрочем, проблемы тут никакой нет: одно основание довольно легко преобразовать в другое. Да-да, один логарифм является ключом ко всем остальным! На этот счет даже есть своя теорема, благодаря которой мы можем, например, взять логарифм по основанию 10 и найти его аналог по основанию b.
Теорема: Для любых положительных значений b и x
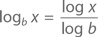
Доказательство: Предположим, что y = logb x. Тогда by = x. Прологарифмируем обе части: log by = log x. Согласно второму замечательному пределу, y log b = log x. Следовательно, y = (log x)/(log b), что и требовалось доказать.◻
ln x = (log x) / (log e) = (log x) / (0,434…) ≈ 2,30 log x
logb x = (log x) / (log 2) = (log x) / (0,301…) ≈ 3,32 log x
Другие лики е
Как и число π, число e широко используется в математике. И, как и π, оно встречается подчас там, где вы совершенно не ожидаете его увидеть. Например, колоколообразная кривая, которую мы уже упоминали в главе 8, имеет формулу
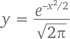
а ее график, изображенный чуть ниже, – наверное, самый важный график в любом статистическом исследовании.

