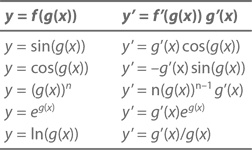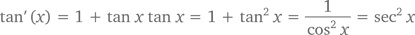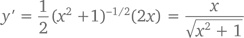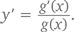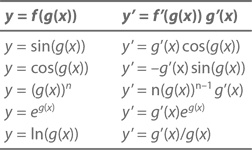Разделим все члены на cos x и решим уравнение для tan' (x):
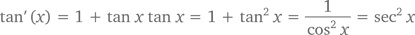
в котором предпоследнее значение получается в результате деления тождества cos 2x + sin 2x = 1 на cos 2x.
Отступление
Доказательство правила дифференцирования частного: Так как u(x)g(x) = f(x), продифференцировав обе части уравнения, в соответствии с правилом дифференцирования произведения получим
u(x) g'(x) + u'(x) g(x) = f'(x)
Умножив все на g(x), получим
g(x) u(x) g'(x) + u'(x) g(x) g(x) = g(x) f'(x)
Заменим g(x) u(x) на f(x) и решим уравнение для u'(x), что приведет нас к искомому результату.◻
Теперь мы умеем дифференцировать многочлены, показательные и тригонометрические функции. Также мы научились дифференцировать их суммы, произведения и частные. Но есть еще сложные функции – функции от функций, с которыми тоже нужно уметь обращаться. Правило дифференцирования сложной функции иначе называют цепным правилом. Согласно ему, например, если f(x) = sin x, а g(x) = x³, то
f(g(x)) = sin(g(x)) = sin(x³)
Не перепутайте: это не то же самое, что
g(f(x)) = g(sin x) = (sin x)³
Теорема (цепное правило): Если y = f(g(x)), то y' = f'(g(x))g'(x).
Например, если f(x) = sin x, а g(x) = x³, то f'(x) = cos x, а g'(x) = 3x². Согласно цепному правилу, при y = f(g(x)) = sin (x³)
y' = f'(g(x))g'(x) = cos(g(x))g'(x) = 3x² cos(x³)
Обобщая, можно сказать, что при y = sin (g(x)) y' = g'(x) cos(g(x)). Та же логика подсказывает нам, что y = cos (g(x)) имеет производную y' = –g'(x) sin (g(x)).
С другой стороны, функция y' = –g'(x) sin (g(x)), согласно цепному правилу, выглядит так:
y' = g'(f(x))f'(x) = 3(f(x)²)f'(x) = 3 sin² x cos x
Обобщим и это: цепное правило говорит нам, что при y = (g(x))n y' = n(g(x))n–1g'(x). А что насчет y = (x3)5?
y' = 5(x3)4(3x²) = 5x12(3x2) = 15x14
что полностью соответствует правилу дифференцирования произведения функций.
Продифференцируем y = √(x2 + 1) = (x² +1)½.
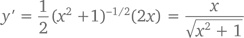
Со степенными функциями дело обстоит ничуть не сложнее. Так как ex является собственной производной, то при y = eg(x) имеем
Например, производная y = ex³ – y' = (3x²)ex³.
Обратите внимание, что функция y = ekx имеет производную y' = kekx = ky. Это одна из причин, почему показательные (экспоненциальные) функции так важны – они появляются, когда скорость роста функции пропорциональна величине ее значения. По этой причине показательные функции часто связаны с процессами в финансовой сфере и в биологии.
Натуральный логарифм ln x обладает одним интересным свойством:
при любом значении x, большем 0. Чтобы найти его, логарифма, производную, воспользуемся цепным правилом. Допустив, что u(x) = ln x, получим eu(x) = x. Продифференцировав обе части этого уравнения, получаем u'(x)eu(x) = 1. Но поскольку eu(x) = x, u'(x) = 1/x. Другими словами, если y = ln x, тогда y' = 1/x. Вновь применив цепное правило, получаем: если y = ln (g(x)), то
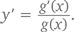
Давайте соберем все найденное с помощью цепного правила в таблицу: