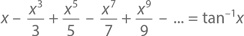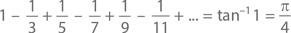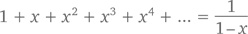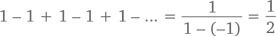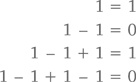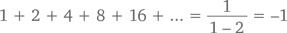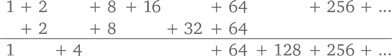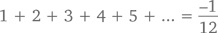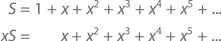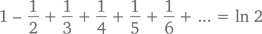
Отступление
Если же заменить x на – x², то при значении x, находящемся между –1 и 1,
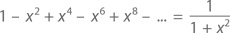
В большинстве учебников по исчислению сказано, что y = tan–1x имеет производную
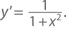 Следовательно, если мы найдем первообразные обеих сторон (не забыв, что tan−10 = 0), то придем к
Следовательно, если мы найдем первообразные обеих сторон (не забыв, что tan−10 = 0), то придем к
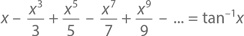
А положив x как величину, стремящуюся к нулю, – и к
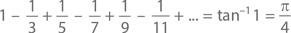
Правильно пользоваться геометрическим рядом мы уже научились. Почему бы немного не попользоваться им неправильно? Формула утверждает, что
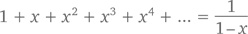
при любом значении x, ограниченным условием, что –1 < x < 1. А что, если набраться смелости и взять x = –1? Тогда наша формула примет следующий вид:
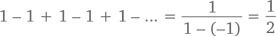
Конечно, это невозможно: при сложении и вычитании целых величин дробь вроде 1/2 просто не может образоваться, даже при сходящейся сумме. С другой стороны, крупица здравого смысла в таком ответе все-таки есть – просто взгляните на промежуточные суммы:
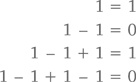
Возьмем другое «незаконное» значение – x = 2. Тогда ряд скажет нам, что
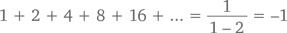
Этот ответ выглядит еще более нелепо, чем предыдущий: как может сумма положительных чисел быть отрицательной? Но зерно истины скрыто и здесь. Помните, в главе 3 мы разбирали случаи, когда положительная величина ведет себя как отрицательная в таких, например, отношениях:
Это привело нас к выводу, что 10k ≡ (–1)k (mod 11).
А вот один очень интересный способ понять 1 + 2 + 4 + 8 + 16 +…, который потребует от нас нестандартного творческого подхода. Вернемся назад к главе 4, в которой мы выяснили, что любое целое может быть представлено в виде уникальной суммы двух степеней двойки. Именно этот принцип лежит в основе двоичной системы счисления – системы, благодаря которой современные компьютеры умеют считать. Причем количество степеней двойки обязательно конечно. Например, в 106 = 2 + 8 + 32 + 64 таких степеней всего четыре. Но предположим, что для нас вдруг стало доступно и бесконечное их количество. Типичное бесконечное целое выглядит как
1 + 2 + 8 + 16 + 64 + 256 + 2048 +…
где каждый член – это степень по основанию 2. К чему это нас приведет, пока неясно, но некоторая закономерность здесь уже прослеживается. Так, эти числа можно складывать, перенося лишние цифры в следующий разряд – как мы всегда и делаем. Например, прибавив к предыдущему ряду число 106, получим
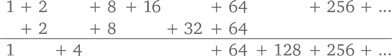
где две двойки предсказуемо дают 4, а две восьмерки – 16. А дальше смотрите, что происходит: этот результат мы прибавляем к следующим 16 и получаем 32. Плюс еще 32 – будет 64. А так как дальше у нас уже есть целых две величины, равные 64, имеем 64 и 128. Все, что выше 256, остается в единственном экземпляре. Теперь попробуйте представить, что произойдет, когда мы прибавим 1 к некой абстрактной «наибольшей» величине.

Мы получим бесконечную цепь реакций, уводящих за пределы уравнения все значения, не связанные степенными отношениями с 2. Следовательно, сумму вполне можно представить как 0. Так как (1 + 2 + 4 + 8 + 16 +…) + 1 = 0, вычитание 1 из обеих частей приведет нас к бесконечной сумме, ведущей себя в точности, как число –1.
Хотите, расскажу вам о своей любимой бесконечной сумме? Вот она:
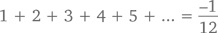
Чтобы доказать это, обратимся к алгебраическим хитростям и так же, как мы делали во втором доказательстве действительности конечного геометрического ряда, сдвинем отдельные элементы. Такой подход отлично срабатывает для конечных сумм, но в применении к суммам бесконечным он дает порой очень странные, порой абсурдные результаты. Применим его для начала к одному из предыдущих тождеств. Сумму запишем дважды – без сдвига и со сдвигом. Получится

Сложим эти два уравнения:
Следовательно, S будет равно 1/2, как мы и рискнули предположить чуть выше, заменив x в геометрическом ряду на –1.
Отступление
Тот же метод можно использовать для быстрого (хотя и не вполне «законного») подтверждения формулы геометрического ряда.
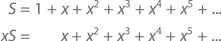
Вычтем одно уравнение из другого:



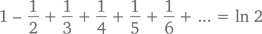
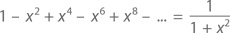
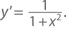 Следовательно, если мы найдем первообразные обеих сторон (не забыв, что tan−10 = 0), то придем к
Следовательно, если мы найдем первообразные обеих сторон (не забыв, что tan−10 = 0), то придем к