Вывод Стандартной модели
Хотя в суперструнах в принципе не существует настраиваемых параметров, струнная теория может предложить решения, удивительно близкие к Стандартной модели с ее пестрым собранием причудливых субатомных частиц и девятнадцатью «гуляющими» параметрами (такими как массы частиц и их силы взаимодействия). Кроме того, в Стандартной модели существует три идентичные (и лишние) копии всех кварков и лептонов, что кажется совершенно бесполезным. К счастью, струнная теория может без напряжения вывести многие качественные характеристики Стандартной модели. В 1984 году Филип Канделас из Техасского университета, Гэри Хоровиц и Эндрю Строминджер из Калифорнийского университета в Санта-Барбаре, а также Эдвард Виттен показали, что если свернуть шесть из десяти измерений струнной теории и при этом сохранить суперсимметрию в оставшихся четырех измерениях, то крошечный шестимерный мир можно описать при помощи того, что математики называют многообразием Калаби – Яу. Взяв несколько примеров из пространств Калаби – Яу, они показали, что симметрию струны можно свести к теории, которая удивительно близка к Стандартной модели.
Таким образом, струнная теория дает нам простой ответ на то, почему в Стандартной модели существует три излишних поколения. В струнной теории количество поколений, или излишеств в кварковой модели, связано с количеством «отверстий», которые мы обнаруживаем в многообразии Калаби – Яу. (Например, возьмем пончик, велосипедную камеру и кофейную чашку – все они являются поверхностями с одним отверстием. В оправе для очков два отверстия. В пространствах Калаби – Яу может существовать произвольное количество отверстий.) Таким образом, просто выбрав многообразие Калаби – Яу, в котором есть определенное количество отверстий, мы можем построить Стандартную модель с различными поколениями лишних кварков. (Поскольку мы никогда не видим пространства Калаби – Яу из-за того, что оно очень маленькое, мы также никогда не видим и того факта, что это пространство, подобно пончику, пронизано отверстиями.) В течение многих лет группы физиков пытались каталогизировать все возможные пространства Калаби – Яу, осознавая тот факт, что топология этого шестимерного пространства определяет кварки и лептоны нашей четырехмерной Вселенной.
М-теория
Всеобщее увлечение струнной теорией, имевшее место в 1984 году, не могло продолжаться вечно. К середине 1990-х годов триумфальное шествие теории суперструн начало сбавлять темп. Легкие проблемы, которые решала эта теория, были уже все выбраны, и остались только сложные. Одной из таких проблем было открытие миллиардов решений струнных уравнений. При компактификации, или свертывании пространства-времени различным образом, струнные решения можно было записывать в любом измерении, а не только в четырех. Каждое из миллиардов струнных решений соответствовало математически непротиворечивой вселенной.
Физики внезапно начали тонуть в струнных решениях. Что примечательно, многие из этих решений выглядели очень похожими на нашу Вселенную. Выбрав подходящее пространство Калаби – Яу, можно было относительно несложно воспроизвести многие из существенных черт Стандартной модели с ее причудливым скоплением кварков и лептонов, даже с ее любопытным набором поколений. Однако чрезвычайно сложной задачей (неразрешенной и по сей день) было обнаружить первоначальную Стандартную модель с определенными значениями ее девятнадцати параметров и тремя излишними поколениями. (Ошеломляющее количество струнных решений, вообще-то, приветствовалось физиками, которые поддерживали идею Мультивселенной, поскольку каждое решение представляет полностью непротиворечивую параллельную вселенную. Однако удручал тот факт, что физики испытывали сложности в обнаружении именно нашей Вселенной в этих джунглях вселенных.)
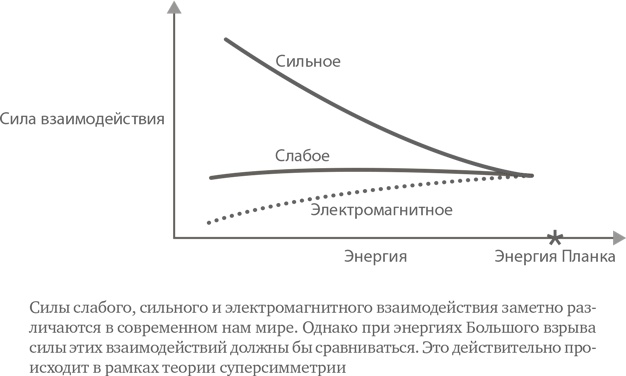
Одной из причин сложности этого предприятия является то, что в конечном счете суперсимметрию все же нужно разрушить, поскольку в нашем мире низких энергий мы этой симметрии не наблюдаем. К примеру, мы не видим в природе сэлектрона – суперпартнера электрона. Если оставить суперсимметрию нетронутой, то масса каждой частицы должна быть эквивалентна массе ее суперчастицы. Физики считают, что суперсимметрия была нарушена, и результатом этого является то, что массы суперчастиц огромны и, таким образом, суперчастицы находятся вне пределов досягаемости современных ускорителей частиц. Но в настоящее время никто еще не предложил правдоподобного механизма для нарушения суперсимметрии.
Дейвид Гросс из Института теоретической физики имени Кавли в Санта-Барбаре заметил, что существуют миллионы и миллионы решений струнной теории в трех пространственных измерениях, что несколько смущает, поскольку нет способа, с помощью которого мы можем выбирать среди них.
Были и другие вопросы: в частности, то, что существовало пять непротиворечивых струнных теорий. Было сложно представить, что Вселенная могла позволять существование пяти отдельных единых теорий поля. Эйнштейн считал, что у Бога не было выбора при создании Вселенной, так почему же Бог должен был создать целых пять вселенных?
Первоначальная теория, основанная на формуле Венециано, описывает то, что называют суперструнной теорией типа I. В теории типа I фигурируют как открытые струны (с двумя концами), так и замкнутые струны (свернутые в окружность). Эту теорию очень активно разрабатывали в начале 1970-х годов. (Используя струнную теорию поля, Киккаве и мне удалось каталогизировать полный набор струнных взаимодействий типа I. Мы показали, что струны типа I требуют пяти взаимодействий. Что касается замкнутых струн, то мы показали, что там необходим только один член взаимодействия.)
Мы с Киккавой также показали, что возможно построение полностью непротиворечивых теорий только с замкнутыми струнами (то есть похожими на петлю). Сегодня такие теории называются струнными теориями типа II, где струны взаимодействуют путем расщепления на две струны меньшего размера (этот процесс напоминает митоз в клетках).
Наиболее реалистичной струнной теорией считается теория гетеротических струн, сформулированная группой ученых из Принстона (в том числе Дейвидом Гроссом, Эмилем Мартинеком, Райаном Ромом и Джеффри Харви). Теория гетеротических струн может содержать в себе группы симметрии, называемые Е (8) ×Е (8) или О (32), которые достаточно велики, чтобы включить в себя теории великого объединения. Теория гетеротических струн полностью основывается на замкнутых струнах. В 1980–1990-е годы, говоря о теории суперструн, ученые подразумевали теорию гетеротических струн, поскольку она достаточно богата, чтобы позволить анализировать внутри нее Стандартную модель и теории великого объединения. Например, группу симметрии Е (8) ×Е (8) можно разбить до симметрии Е (8), а затем – Е (6), которая, в свою очередь, достаточно велика, чтобы включать симметрию SU (3) ×SU (2) ×U (l) Стандартной модели.
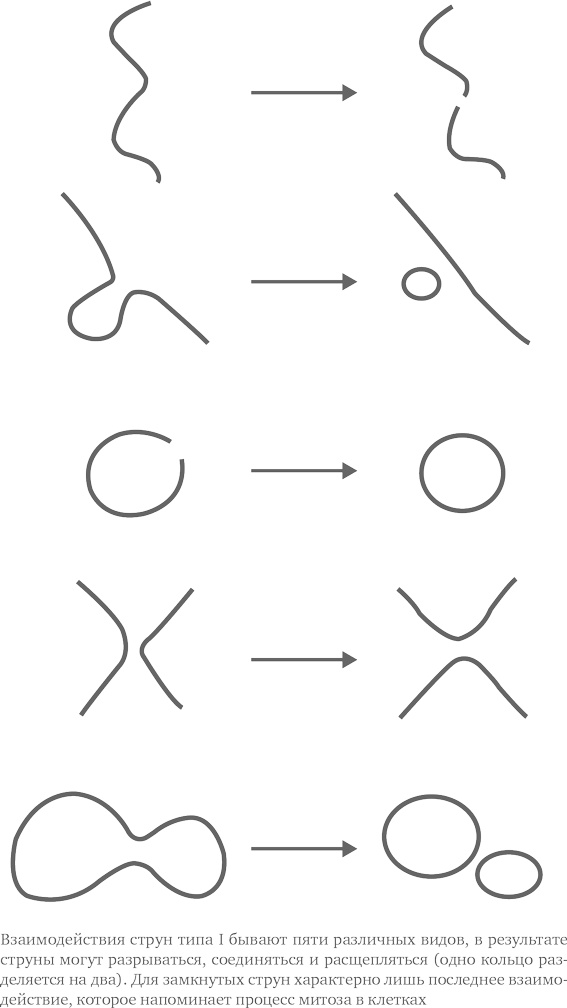
Загадка супергравитации
Вдобавок к наличию пяти теорий суперструн существовал еще один насущный вопрос, позабытый в погоне за решением струнной теории. В 1976 году три физика – Питер ван Ньювенхейзен, Серджо Феррара и Дэниел Фридман, – в то время работавшие в Государственном университете Нью-Йорка в Стоуни-Брук, обнаружили, что первоначальная теория гравитации Эйнштейна могла стать суперсимметричной, если ввести в нее всего лишь одно новое поле – суперпартнер первоначального гравитационного поля со спином 3/2 (названное гравитино, что означает «маленький гравитон»). Эта новая теория получила название теории супергравитации. В ее основе лежали точечные частицы, а не струны. В отличие от теории суперструн, где существовала бесконечная последовательность нот и резонансов, в теории супергравитации было всего лишь две частицы. В 1979 году Юджин Креммер, Джоэл Шерк и Бернар Джулия из французской Высшей технической школы показали, что самая общая теория супергравитации может быть записана в одиннадцати измерениях. (При попытках записать теорию супергравитации в двенадцати или тринадцати измерениях возникали математические противоречия.) В конце 1970-х – начале 1980-х годов считалось, что теория супергравитации вполне могла бы оказаться мифической единой теорией поля. Теория супергравитации даже вдохновила Стивена Хокинга на слова о том, что виден невдалеке «конец теоретической физики» (в ходе его инаугурационной лекции в Кембриджском университете, когда он встал во главе той самой кафедры математики, которую в свое время возглавлял сам Исаак Ньютон). Но супергравитация вскоре столкнулась с теми же проблемами, какие погубили и предыдущие теории. Хотя в теории супергравитации было меньше противоречий, чем в обычной теории поля, ей не хватало завершенности, и было много потенциальных аномалий. Как и все остальные теории поля (за исключением струнной теории), она рассыпалась на глазах у ученых.

