Итак, этот способ отбора, похоже, не работает.
К счастью, есть более удачный подход.
Давайте представим себе язык, в котором есть только два верных предложения, и каждый твит должен быть одним из этих предложений. Это:
В пятом стойле есть лошадь
и
В моем доме полно ловушек.
Тогда лента вашего «Твиттера» выглядела бы вот так:
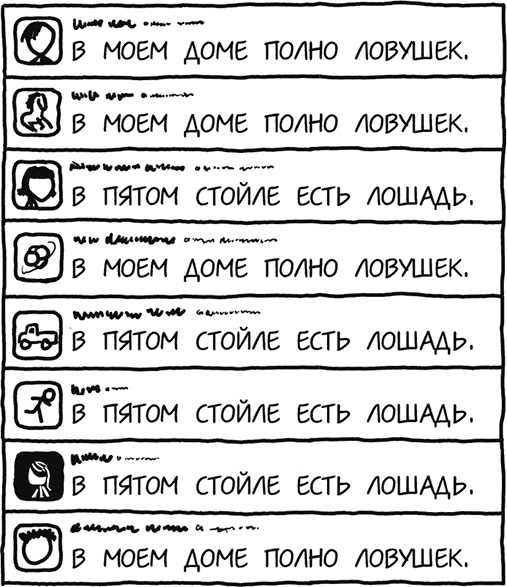
Эти сообщения довольно длинные, но в них не очень много информации – они только показывают, выбрал человек сообщение про ловушки или про лошадь. По сути, это двоичный код – цифра 0 или цифра 1. Хотя здесь много букв, для читателя, владеющего этим языком, каждый твит содержит лишь один бит информации.
Этот пример подводит нас к важной идее о том, что информация фундаментально связана с неуверенностью получателя в содержании сообщения и его неспособностью предсказать это содержание заранее.
Клод Шэннон – который практически в одиночку изобрел современную теорию информации – придумал хитрый метод, чтобы измерять информационную содержательность языка. Он показывал группам людей образцы типичного английского текста, которые были произвольно оборваны, и предлагал угадать, какая буква последует дальше.
Наши города рискуют просто утонуть в информации!
Основываясь на частоте верных догадок – и сложном математическом анализе, – Шэннон определил, что информационная насыщенность типичного письменного английского составляет 1–1,2 бита на букву. Это значит, что хороший алгоритм сжатия должен позволять сжать английский текст в кодировке ASCII, в котором восемь бит на букву, примерно до одной трети изначального объема. И в самом деле, если применить к электронной книге в формате .txt хороший архиватор, примерно это и произойдет.
Если фрагмент текста содержит n бит информации, в определенном смысле это значит, что есть 2ⁿ сообщений, которые он может передавать. Конечно, не обошлось без математического жонглирования (в частности, в том, что касается длины сообщения и штуки под названием «расстояние единственности»), но суть в том, что предположительное количество различных осмысленных твитов на английском составляет 2140×1,1 = 2 × 1046, а не 10200 или 10800.
И сколько же времени потребуется миру, чтобы прочесть их все вслух?
Чтение 2 × 1046 твитов займет у человека порядка 1047 секунд.
Неважно, читает ли их один человек или миллиард, – этих твитов так много, что нельзя прочесть сколько-нибудь существенную их часть, даже если читать все то время, что существует Земля.
Давайте лучше вернемся к птичке, которая точит клюв о скалу. Предположим, что раз в тысячу лет птица откалывает от скалы маленький кусочек и, улетая, уносит на себе несколько десятков крупиц камня. (Нормальная птица оставила бы на скале вещества клюва, чем унесла бы камня, но в этой истории нет ничего нормального, так давайте просто продолжим в том же духе.)
Предположим, вы читаете твиты вслух по 16 часов в день, ежедневно. И за вашей спиной каждую тысячу лет прилетает птица и соскребает несколько невидимых крупиц с вершины скалы.
Когда скала будет сточена до основания, пройдет один день вечности.
Скала появляется снова, и цикл возобновляется еще на один день вечности. 365 дней вечности = каждый из них длиной 10³² лет – составляют год вечности.
Сотня лет вечности, за которые птица сточит 36 500 скал, составит столетие вечности.
Но столетия не хватит. Как и тысячелетия.
Чтобы прочесть все твиты, вам потребуется десять тысяч лет вечности.

Этого времени достаточно, чтобы увидеть, как разворачивается вся история человечества с момента изобретения письменности и до сего дня – если каждый день будет занимать столько времени, сколько нужно птичке, чтобы сточить скалу.

Кажется, что 140 знаков – это немного, но нам всегда будет что сказать.
LEGO-мост
ВОПРОС: А что, если построить мост от Лондона до Нью-Йорка из кирпичиков конструктора Lego? Существует ли вообще в мире столько деталей Lego?
– Джерри Петерсон
ОТВЕТ: Начнем с чуть менее амбициозной задачи.
Наводим мосты
В мире совершенно точно произведено достаточно кирпичиков Lego
[119], чтобы соединить Нью-Йорк и Лондон. Если измерять средствами LEGO
[120], то Нью-Йорк и Лондон разделяют 700 миллионов шипов. Это значит, что, если кирпичики расположить так…

…потребуется 350 миллионов кирпичиков, чтобы соединить два города. Такой мост будет крайне непрочен, и вряд ли он выдержит вес чего-то более серьезного, чем LEGO®-человечек
[121], но для начала неплохо.
За много лет было произведено более 400 миллиардов деталей Lego
[122]. Но какую часть из них составляют кирпичики, годные для постройки моста, а какую – маленькие шлемы для лего-человечков, вечно теряющиеся где-то в ворсе ковра?







