После того как мы подбросили правильную монету 7 млрд раз, мы можем ожидать, что в половине из бросков выпадет орел. Но можем ли мы ожидать серию из миллиона орлов последовательно? Машина для бросания монеты показывает нам, что, несмотря на случайность траектории движения монеты, ее можно заставить выпадать орлом в 100 % случаев.
Вероятность падения правильной монеты орлом вверх – 1/2. Благодаря математике мы знаем, что по мере увеличения числа бросков монеты отношение орлов к решкам постепенно приближается к 1. Эвристическая оценка нарушает смысл последнего предложения, превращая его в утверждение того, что длинная серия решек неким образом окажется сбалансирована серией орлов. Легко стать жертвой ошибочного впечатления, что если одна из сторон очень долго не выпадала, то шансы ее появления увеличиваются с каждым ходом, хотя мы знаем, что теоретически каждый раз, когда брошена монета, шансы за и против каждого из исходов совершенно одинаковы – монета может с равным успехом выпасть «орлом» или решкой. Дело в том, что люди путают исходы событий и частотность.
Длинные серии орлов могут иметь место. Я наблюдал очень длинные серии орлов. На интуитивном уровне нам может казаться странным, что происходит нечто подобное. Предположим, что вы бросаете монету 10 раз и орел выпадает 7 раз. Пропорция орлов к решкам тогда составит 7 к 3. Бытовые представления подсказывают нам, что в ходе следующих десяти бросков решка должна выпасть больше шести раз, чтобы сбалансировать превысившее ожидания число ранее выпавших орлов. Но у монеты нет памяти о том, что с ней произошло ранее, есть только история результатов, записанная наблюдателем. Ничто не мешает монетке выпасть орлом в ходе следующих 500 бросков, однако, если это произойдет, мы сильно удивимся.
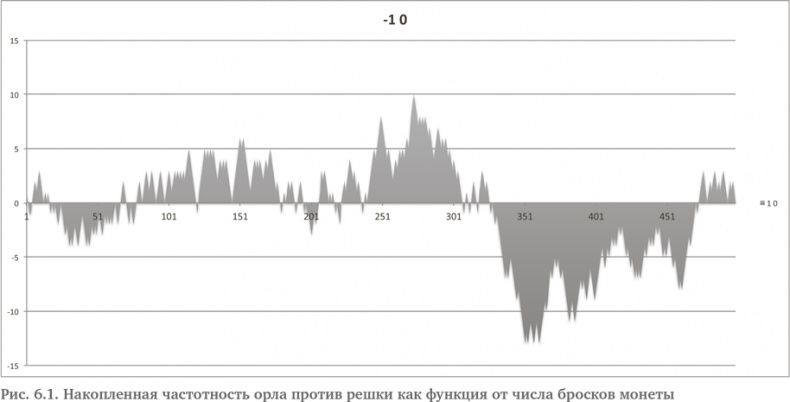
На рис. 6.1 представлен сгенерированный компьютером совокупный результат 500 бросков монеты (+1 для каждого орла, – 1 для каждой решки). Горизонтальная линия обозначает 0. Орел и решка перехватывают лидерство друг у друга. Это как гонка двух лошадей с равными шансами. Этого вполне можно ожидать. Суждение, основанное на бытовых представлениях, говорит в пользу того, что график должен был бы прыгать около нулевой линии. Однако чаще всего такие графики подолгу остаются с одной стороны от нуля.
Абсолютная случайность как теория и та же абсолютная случайность в реальном, физическом мире – не одно и то же. Пронумерованные шарики для пинг-понга, которые кружатся в акриловой сфере, а потом вылетают по специальной трубке, движутся вовсе не случайным образом, но для стороннего наблюдателя они определенно выдают случайные числа. Бросок монеты, который определяет, кто начинает матч в американском футболе, весьма далек от того, чтобы быть случайным. На самом деле результат броска монеты – вопрос элементарной физики. Уже созданы машины, которые могут бросать монету сколь угодно долго – тысячу раз, миллион – и всегда выпадает орел.
Недавние эксперименты показывают, что монеты, даже правильные монеты, склонны выпадать той же стороной, с которой начинается бросок, а исход броска зависит от угла между нормалью к плоскости монеты и вектора углового момента. Другими словами, полет монеты определяется начальными условиями. Диаконис, Холмс и Монтгомери построили машину, которая подбрасывает монеты посредством пружинно-храпового механизма
{62}. С этой машиной любая монета, движение которой начинается из положения «орел», всегда (в 100 % случаев) выпадает орлом вверх. Так что результат броска монеты определяется физикой, а не случайностью. Рука того, кто бросает, и множество переменных внешней среды вызывают разнообразные исходы, которые кажутся случайными.
Но мы можем обмануться иллюзией того, что монета крутится, в то время как на самом деле она просто прецессирует в воздухе, как медленно вращающийся гироскоп. Ориентация монеты в полете определяется вектором ее углового момента, который может быть всегда направлен вверх. Итак, монета, которая начинает движение из положения «орел», может всегда выпадать орлом, поскольку следует определенной траектории, хотя кажется, что орел и решка крутятся.
Когда речь идет о бросании монеты в реальных условиях, а исходы событий определяются малейшим воздействием от землетрясений, происходящих в тысяче километров от нас, или надоедливой бабочкой-смутьянкой над Тихим океаном, все иначе. Но иначе не значит объяснимо или постижимо. Падение монеты очень даже может быть случайным, но наше человеческое представление о случайности часто не в ладах с нашим же предчувствием относительно случайных исходов. Поскольку у монеты нет памяти о предыдущих исходах, нам не следовало бы удивляться, если она выпадет решкой 100 раз подряд, но мы все же удивляемся.
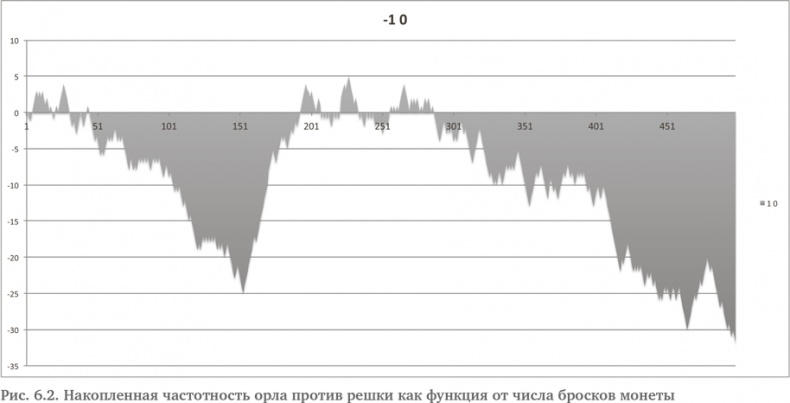
На рис. 6.2 мы увидим странную историю. Исходы вполне следуют ожиданиям вплоть до 45-го броска, когда решка вдруг перехватывает инициативу примерно на 105 следующих бросков! Затем идет достаточно долгий период, когда лидирует орел, и совокупное значение опять приближается к 0. Но около 286 броска решка опять надолго вырывается вперед. Не то чтобы события не согласовывались с нашими интуитивными ожиданиями. Действительное отношение орлов к решкам наверняка приблизится к 1 в ходе значительно более долгого времени, но в краткосрочной перспективе этого не происходит. За 500 бросков решка выпала только на 12 раз больше, чем орел. Это достаточно мало, но последовательности орлов и решек могут расходиться значительно сильнее в совокупных результатах. Например, рассмотрим следующее испытание, показанное на рис. 6.3.
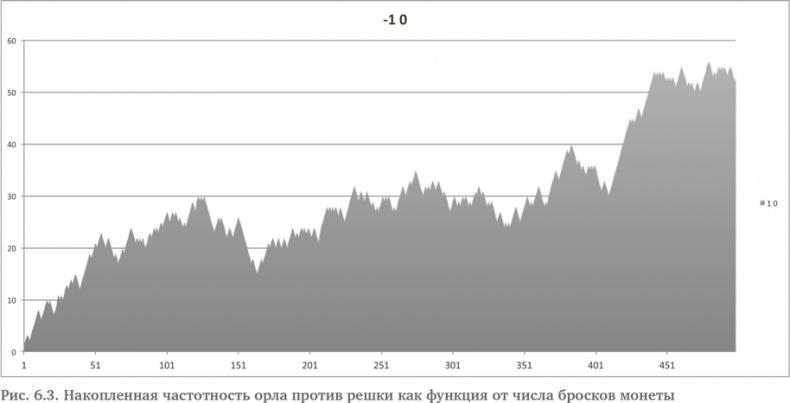
Орел полностью контролирует ситуацию. Совокупный исход показывает, что орел ведет настолько уверенно на протяжении всей серии бросков, что кажется, будто решка никогда уже не вырвется вперед.
Результаты компьютерной модели 1 млн бросков разобраны в табл. 6.1. Отношение k/N, где k – число успешных исходов, а N – число испытаний, называют эмпирической частотой успешности испытаний. В правой колонке в табл. 6.1 приведены абсолютные значения разности между эмпирической частотой успешности испытаний и 1/2 – математически предсказанной частотой успешности испытаний.
Слабый закон больших чисел не исключает, что какие-то маловероятные события будут происходить часто на раннем этапе игры или на более поздних. На самом деле, даже если коэффициент успешности приближается к математически предсказанному, нет гарантии, что он таким и останется. Чуть более сильный математический результат говорит нам, что, хотя коэффициент успешности может сходиться к теоретически вычисленному, действительные значения коэффициента склонны к довольно странному поведению по мере увеличения числа испытаний. Контринтуитивно, но это так.





