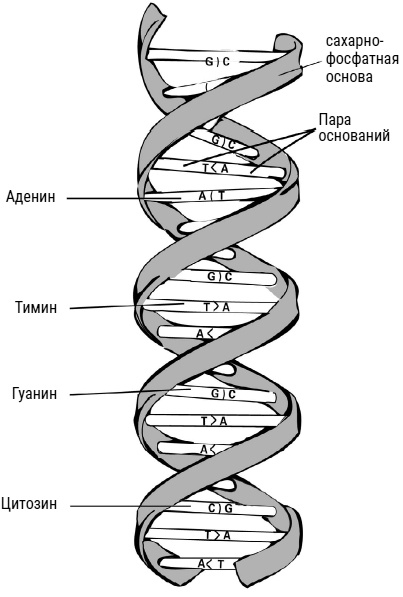
Рис. 58

Рис. 59
Всем этим развязыванием и распутыванием занимаются особые вещества – ферменты
[150]. Ферменты умеют пропускать цепочки ДНК друг через друга – для этого они на время разрывают их и связывают освободившиеся концы по-другому. Знакомо, правда? Именно такие хирургические операции предложил Конвей для распутывания математических узлов (как изображено на рис. 56). Иначе говоря, с топологической точки зрения ДНК – сложный узел, и для репликации и транскрипции нужно, чтобы ферменты его развязали. С помощью теории узлов можно понять, насколько трудно распутать ДНК, и таким образом можно изучать свойства ферментов, которые отвечают за распутывание. Мало того, при помощи средств экспериментальной визуализации – электронной микроскопии и электрофореза в полиакриламидном геле – ученые могут наблюдать и измерять изменения в образовании узлов и сцеплений ДНК, вызванные ферментами (на рис. 59 показана электронная микрофотография узла ДНК). Помимо всего прочего, изменение числа пересечений в узле ДНК дает биологам возможность оценить скорость реакций с участием ферментов: на сколько пересечений в минуту может повлиять фермент в той или иной концентрации.
Однако теория узлов нашла неожиданное применение не только в молекулярной биологии. Об узлах речь идет и в теории струн – современной попытке сформулировать универсальную теорию, объясняющую все взаимодействия в природе.
Вселенная по струнке?
Гравитация – это сила, которая действует на самых больших масштабах. Она удерживает звезды в галактиках, она влияет на расширение Вселенной. Замечательная теория, описывающая гравитацию, – это общая теория относительности Эйнштейна. А в глубинах атомных ядер владычествуют совсем другие силы и совсем другая теория. Сильное ядерное взаимодействие связывает частицы под названием кварки, и из них создаются знакомые многим протоны и нейтроны – главные компоненты видимого вещества. Поведение частиц и сил в субатомном мире регулируется законами квантовой механики. Едины ли законы для кварков и галактик? Физики считают, что законы должны быть едины, хотя пока еще не понятно, почему. Уже несколько десятков лет физики пытаются построить «Теорию Всего» – всеобъемлющее описание законов природы. В частности, они хотели бы ликвидировать разрыв между большим и малым при помощи квантовой теории гравитации – примирить общую теорию относительности с квантовой механикой. На данный момент лучшим кандидатом на звание Теории Всего считается теория струн
[151]. Первоначально эта теория была разработана для ядерного взаимодействия как такового, но в 1974 году физики Джон Шварц и Джоэль Шерк привлекли к ней внимание широкой физической общественности уже в ином качестве. Основная идея теории струн довольно проста. Элементарные субатомные частицы, например электроны и кварки – вовсе не точечные сущности, не имеющие структуры. Напротив, элементарные частицы представляют разные виды вибраций одной и той же фундаментальной струны. Согласно этой теории, космос наполнен тоненькими и гибкими, будто резиновыми, петлями. Скрипичную струну можно ущипнуть и получить разные гармонии, точно так же разные вибрации этих переплетенных струн соответствуют разным частицам вещества. Иначе говоря, мир подобен симфонии.
Поскольку струны – это замкнутые петли, движущиеся в пространстве, то с течением времени они заметают области (так называемые мировые листы) цилиндрической формы (рис. 60). Если струна испускает другие струны, цилиндр разветвляется, образуется что-то вроде рогульки. Если взаимодействует сразу много струн, получается сложная система переплетенных изогнутых цилиндров – вроде сплавленных друг с другом пышек.
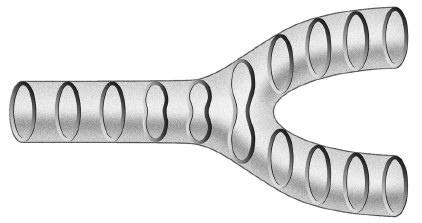
Рис. 60
Изучая сложные топологические структуры подобного рода, специалисты по теории струн Хироси Оогури и Кумран Вафа обнаружили неожиданную связь между количеством таких пышек, сложными геометрическими свойствами узлов и многочленом Джонса (Ooguri and Vafa 2000). Но еще раньше Эдвард Виттен, один из главных игроков на поле теории струн, выявил соотношение между многочленом Джонса и самой основой теории струн – так называемой квантовой теорией поля (Witten 1989). Затем модель Виттена переосмыслил с точки зрения чистой математики Майкл Атья
[152]. Так что теория струн и теория узлов живут в идеальном симбиозе. Теория струн, с одной стороны, получила много полезных результатов при помощи теории узлов, а с другой – и сама натолкнула на интересные открытия в этой области.
В гораздо более широком масштабе теория струн ищет объяснения самой сущности вещества – причем движется примерно в том же направлении, что и Томсон, когда придумывал модель атома. Томсон (ошибочно) полагал, что узлы могут дать ответ на вопрос о строении атомов. И вот по интересной прихоти судьбы специалисты по теории струн обнаружили, что узлы и в самом деле позволяют сделать некоторые выводы.
История теории струн – это великолепный пример нежданного могущества математики. Как я уже упоминал, даже «активная» сторона эффективности математики сама по себе, когда ученые генерируют математические теории, необходимые для описания наблюдаемых физических феноменов, иногда – если речь заходит о точности – приносит невероятные сюрпризы. Рассмотрим вкратце одну область физики, где важную роль играют обе стороны математики, и «активная», и «пассивная», – область, примечательную именно тем, какой поразительной точности удалось там добиться.
С аптечной точностью
Галилей и другие итальянские ученые-экспериментаторы вывели законы падения тел, а Ньютон взял эти законы в сочетании с законами движения планет, которые открыл Кеплер, и на основе объединенных данных сформулировал математический закон всемирного тяготения. При этом Ньютону пришлось разработать совершенно новую область математики – интегральное и дифференциальное исчисление, – которое позволило в полной мере воплотить все качества законов движения и тяготения. С учетом погрешности современных Ньютону экспериментов и наблюдений, он сумел проверить собственный закон всемирного тяготения лишь с точностью хуже, чем четыре процента. А впоследствии оказалось, что по точности этот закон превосходит все мыслимые ожидания. К концу 50-х годов ХХ века погрешность экспериментов составляла менее одной десятитысячной доли процента.





