Однако главный вопрос, на который нам нужно ответить в контексте этой книги, состоит не в том, придавали ли ранние цивилизации какое-либо символическое или мистическое значение пентаграммам и правильным пятиугольникам, а в том, осознавали ли эти цивилизации особые геометрические свойства этих фигур, а в особенности – золотое сечение.
В те дни, как не был прахом Вавилон
[3]Исследования клинописных табличек, датируемых II тысячелетием до н. э. и найденных в 1936 году в Сузах в Иране, практически не оставляют сомнений, что вавилоняне времен первой династии знали формулу, позволяющую хотя бы приблизительно вычислить площадь правильного пятиугольника. Интерес вавилонян к пятиугольнику, вероятно, объяснялся тем простым фактом, что это фигура, которая получается, если прижать к глиняной табличке кончики всех пяти пальцев. На одной табличке из Суз мы читаем: «1 40, постоянная пятисторонней фигуры». Поскольку у вавилонян была принята шестидесятеричная система счисления, числа 1 40 следует толковать как 1 + 40/60, то есть площадь правильного пятиугольника со стороной 1 равна 1,666… На самом деле площадь правильного пятиугольника со стороной 1 не так уж далека от этой величины – 1,720. Вавилоняне вычислили подобное приближенное значение и для числа π – отношения длины окружности к диаметру. По сути дела, вычисление приближенного значения и числа π, и площади правильного пятиугольника опирается на одно и то же соотношение. Вавилоняне предположили, что периметр любого правильного многоугольника (фигуры с любым количеством равных сторон и равных углов) равен радиусу окружности, в которую вписан этот многоугольник, умноженному на 6 (рис. 12). На самом деле это совершенно справедливо для правильного шестиугольника (он и изображен на рис. 12), поскольку все шесть треугольников, из которых он состоит, равнобедренные. Согласно вычислениям вавилонян, число π равнялось 3 + 1/8, то есть 3,125. И правда, очень неплохое приближение, ведь значение числа π составляет 3,14159… Для правильного пятиугольника неточное предположение, что «периметр равен шести радиусам», дает приблизительное значение площади в 1,666… – то есть тот самый коэффициент, который мы видим на табличке из Суз.
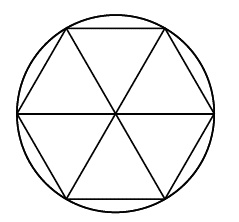
Рис. 12

Рис. 13
Несмотря на эти важные ранние открытия в математике и на теснейшую связь системы пентаграммы-пятиугольника и золотого сечения, нет ни малейших математических свидетельств, что вавилоняне знали о золотом сечении. Тем не менее, в некоторых книгах и статьях утверждается, что золотое сечение будто бы наблюдается в пропорциях ассиро-вавилонских стел и барельефов. Например, в увлекательной книге Майкла Шнайдера «Конструирование Вселенной. Руководство для начинающих» (Michael Schneider. A Beginner’s Guide to Constructing the Universe) утверждается, что вавилонская стела (рис. 13) с изображением жрецов, которые ведут инициируемого на «встречу» с богом Солнца, «во многих отношениях связана с золотым сечением». А в статье, опубликованной в 1976 году в журнале «The Fibonacci Quarterly», искусствовед Хелен Хедиан пишет, что барельеф ассирийского крылатого полубога, созданный в IX в. до н. э. (в настоящее время он хранится в музее Метрополитен в Нью-Йорке) идеально вписывается в прямоугольник с соотношением сторон, соответствующим золотому сечению. Более того, Хедиан предполагает, что четкие контуры крыльев, ног и клюва также построены в соответствии с долями числа φ. Нечто подобное Хедиан говорит и о вавилонской «Умирающей львице» из Ниневии, которую датируют примерно 600 г. до н. э. и которая сейчас хранится в Британском музее в Лондоне.
Так можно ли сказать, что при создании всех этих артефактов из Междуречья действительно было использовано золотое сечение, или это просто научное заблуждение?
Чтобы ответить на этот вопрос, нам придется ввести какие-то критерии, которые позволят определить, истинны или ложны те или иные заявления о появлении золотого сечения. Очевидно, что присутствие золотого сечения можно доказать безо всяких сомнений лишь в том случае, если сохранилась какая-то документация, из которой следует, что художники или архитекторы сознательно прибегали к этому соотношению. К несчастью, вавилонские таблички и барельефы никакой подобной документацией не подкрепляются.
Разумеется, преданный поклонник золотого сечения возразит на это, что отсутствие доказательств не есть доказательство отсутствия, и что достаточным подтверждением применения золотого сечения могут стать параметры произведения искусства сами по себе. Однако, как мы вскоре увидим, попытки найти золотое сечение в параметрах предметов – затея, которая ни к чему хорошему не приводит. Позвольте подтвердить это простым примером. На рис. 14 приведен чертеж маленького телевизора, который стоит у меня в кухне. На чертеже указаны некоторые измерения – их я сделал сам. Легко видеть, что соотношение толщины и высоты задней части телевизора равно 10,6/6,5 дюймов, то есть 1,63, а соотношение ширины передней части и высоты экрана 14/8,75 = 1,6, то есть оба эти соотношения, несомненно, очень близки к золотому сечению – 1,618…. Означает ли это, что изготовители телевизора решили выстроить его архитектуру в соответствии с золотым сечением? Ясно, что нет. Это пример просто показывает две главные ошибки тех, кто ищет золотое сечение в архитектуре или в произведениях искусства на основании одних размеров: (1) подсчеты всегда несколько натянуты, а (2) неточность измерений не учитываются. Каждый раз, измеряя параметры какой-то относительно сложной структуры (картины, стелы, телевизора), вы получаете в свое распоряжение большой набор длин – есть из чего выбрать. И есть чем пренебречь – можно не обращать внимания на остальные детали изучаемого предмета, так что нужно лишь набраться терпения и по-всякому играть и манипулировать числами, и тогда обязательно найдется какая-нибудь интересная комбинация. Вот и я, исследуя телевизор, «открыл» некоторые измерения, отношения которых близки к золотому сечению.
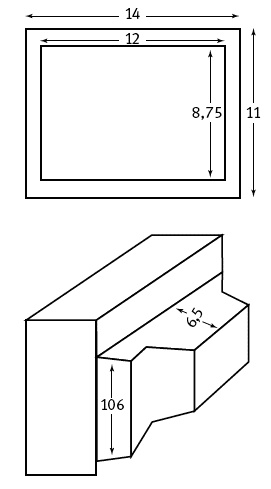
Рис. 14
Второе обстоятельство, которое часто не принимают во внимание излишне рьяные любители золотого сечения, состоит в том, что я измерял все эти длины с некоторой погрешностью. Важно понимать, что любая неточность в измерении длин приводит к еще большей неточности в вычислении их отношения. Представьте себе, например, что вы измерили две длины по 10 дюймов с погрешностью в 1 %. Это значит, что результат измерения каждой длины может попасть в промежуток от 9,9 до 10,1 дюймов. Отношение этих длин может получиться даже 9,9/10,1 = 0,98, то есть погрешность окажется уже в 2 %, вдвое больше, чем при измерении каждой длины по отдельности! Таким образом, излишне страстные почитатели золотого сечения вполне могут изменить два параметра на 1 % – а это повлияет на итоговое отношение уже на 2 %.





