Пока Барт пытается понять, что такое луны Нептуна и шары Юпитера, другой ученик делает еще одно, не менее запутанное предложение: «А я поменяю тысячу пиколитров своего молока на четверть пинты твоего». Еще одна бессмысленная головоломка, предназначенная исключительно для того, чтобы унизить новичка.
На следующий день настроение Барта портится еще больше, когда он узнает, что первый урок – математика. Учительница предлагает ученикам задачу, и именно в этот момент мы сталкиваемся с первым примером явной математической шутки в «Симпсонах». Стоя у доски, учительница пишет уравнение и говорит: «Таким образом, y равняется r в кубе, и если вы правильно определите уровень изменения в этом графике, то, думаю, будете приятно удивлены».
Далее наступает короткая пауза, после которой все ученики (кроме одного) находят ответ и начинают смеяться. Пока одноклассники Барта смеются, учительница пытается ему помочь и пишет на доске пару подсказок. В конце концов она записывает полное решение задачи. Но Барт продолжает недоумевать, и тогда учительница поворачивается к нему и говорит: «Ты разве не понял, Барт? Производная dy равняется трем r квадрат dr на три, или r квадрат dr, или r dr r».
Объяснения учительницы отображены на представленном ниже схематическом рисунке. Однако я подозреваю, что даже при наличии этой визуальной подсказки вы можете пребывать в не меньшем замешательстве, чем Барт. Если это действительно так, советую обратить внимание на последнюю строку на доске (r dr r). В ней содержится не только ответ задачи, но и вся соль шутки. Здесь возникают два вопроса: почему строка r dr r такая смешная и почему она является решением математической задачи?
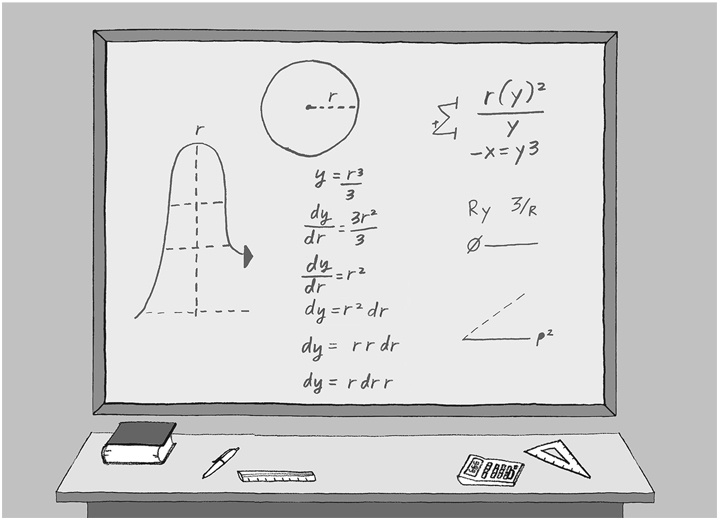
Когда в эпизоде «Барт – гений» учительница ставит задачу по матанализу, она использует нестандартную схему и непоследовательное представление символов, а также допускает ошибку. Тем не менее ей удается получить правильный ответ. На рисунке воспроизведено то, что писала учительница на доске, за одним исключением: здесь задача сформулирована более четко. Шесть строк, расположенных под окружностью, – это важные уравнения.
Класс смеется, потому что строка r dr r звучит как har-de-har-har – выражение, которое употребляется, чтобы продемонстрировать сарказм в ответ на плохую шутку. Фразу har-de-har-har популяризировал Джеки Глисон, сыгравший Ральфа Крэмдена в классическом ситкоме 1950-х The Honeymooners («Новобрачные»). А в 1960-х годах она получила еще большую известность, после того как анимационная студия Hanna-Barbera придумала персонажа по имени Hardy Har Har (Выносливый Хар Хар) – угрюмую гиену в плоской шляпе с полями, которая в компании со львом Липпи стала героем десятков мультфильмов.
Таким образом, фраза har-de-har-har – своего рода каламбур на тему r dr r, но почему она является решением математической задачи? Дело в том, что задача относится к пользующейся дурной славой области математики под названием «математический анализ» – дисциплины, вселяющей ужас в сердца многих подростков и вызывающей кошмарные воспоминания у людей постарше. Как объясняет учительница во время постановки задачи, цель математического анализа – «определить уровень изменения» одной величины, в данном случае y, по сравнению с изменениями другой величины, r.
Если вы помните правила матанализа
[5], то вам будет нетрудно понять логику этой шутки и получить правильный ответ: r dr r. Если же вы относитесь к числу тех, кто приходит от матанализа в ужас или страдает от тяжелых воспоминаний, не волнуйтесь: сейчас еще не время начинать длинную лекцию о тонкостях этого предмета. Вместо этого нам предстоит найти ответ на более насущный вопрос: почему авторы «Симпсонов» включают сложные математические концепции в свой комедийный сериал?
В состав основной команды, работавшей над первым сезоном «Симпсонов», входило восемь умнейших комедийных сценаристов Лос-Анджелеса. Они стремились писать сценарии, в которых бы упоминались продвинутые концепции из всех областей человеческого знания, и матанализ относился к числу их главных приоритетов, поскольку два сценариста были страстными поклонниками математики. Именно эти два нерда придумали шутку с r dr r; и именно им следует отдать должное за то, что сериал «Симпсоны» стал орудием распространения математических шуток.
С одним из них, Майком Рейссом, я познакомился во время встречи со сценаристами «Симпсонов». Точно так же как Мэгги, он продемонстрировал свои математические способности еще будучи малышом, когда складывал кубики. Рейсс отчетливо помнит момент, когда понял, что кубики подчиняются бинарному закону в том смысле, что два самых маленьких кубика имеют такой же размер, как один средний; два средних кубика такого же размера, как один большой, а два больших кубика равны одному очень большому кубику.
Как только Рейсс научился читать, его интерес к математике перерос в любовь к головоломкам. Особенно его привлекали книги Мартина Гарднера, величайшего специалиста по математическим играм и развлечениям. Игривый подход Гарднера к математическим задачам нравился людям всех возрастов. Его друг однажды сказал: «Мартин Гарднер превратил тысячи детей в математиков, а тысячи математиков – в детей».
Сначала Рейсс прочитал книгу The Unexpected Hanging and Other Mathematical Diversions («Неожиданное зависание и другие математические отклонения»), а затем начал тратить все свои карманные деньги на другие книги Гарднера. В возрасте восьми лет Рейсс написал Гарднеру письмо, в котором признался, что он его большой поклонник, а затем рассказал об одном интересном наблюдении, касающемся палиндромных квадратов, а именно, что эти числа содержат, как правило, нечетное количество цифр. Палиндромные квадраты целых чисел – это просто квадраты целых чисел, которые имеют такой же вид, если их записать в обратном порядке, например 121 (11²) или 5 221 225 (2285²). Восьмилетний мальчик оказался абсолютно прав, поскольку существует тридцать пять таких чисел меньше 100 миллиардов, и только в одном из них четное количество цифр – 698 896 (836²).
Рейсс неохотно признался мне, что его письмо Гарднеру также содержало один вопрос. Он спрашивал, является ли количество простых чисел конечным или бесконечным. Сейчас он несколько смущенно вспоминает об этом: «Я отлично помню то письмо и тот глупый, наивный вопрос».
Большинство людей посчитали бы, что Рейсс слишком строг к себе, восьмилетнему, потому что ответ далеко не так очевиден. Его вопрос основан на факте, что у каждого целого числа есть делители – числа, на которые оно делится без остатка. Простое число примечательно тем, что у него только два делителя – 1 и само число (так называемые тривиальные делители). Таким образом, 13 – это простое число, потому что у него нет нетривиальных делителей, а 14 – нет, поскольку его можно разделить на 2 и 7. Все числа являются либо простыми (например 101), либо их можно разделить на простые делители (например 102 = 2 × 3 × 17). Между числами 0–100 существует 25 простых чисел, между 100–200 – 21 простое число, а между 200–300 – всего 16 простых чисел, стало быть, количество простых чисел уменьшается. Тем не менее закончатся ли они со временем или их список бесконечен?



