1.27. Размеры бумаги
Математические понятия: геометрия, пропорции
В следующий раз, когда воспользуетесь ксероксом, взгляните на листы бумаги еще раз: для их дизайна ушло немало математического планирования. Размеры, согласованные с Международной организацией по стандартизации (ИСО) специально для форматов А и В, были созданы на основе особой геометрии, которая имеет свои преимущества, когда вы делаете копии.
Особой характеристикой форматов А и В является соотношение двух концов данного листа бумаги. Для двух форматов коэффициент ширины к длине составляет 1:√2. Это значит, что каждый лист А4 составляет половину площади листа А3. А лист А3 составляет половину площади листа А2. Использование √2 означает, что каждый формат бумаги имеет одинаковое отношение ширины к высоте; каждый формат является идеально масштабированной версией большего или меньшего формата бумаги. Например, формат А4 – который примерно соответствует американскому формату Letter – имеет ширину 210 мм и длину 297 мм. Соответствующие размеры формата А3 будут составлять 297 и 420 мм.
В результате, если вы используете ксерокс и вам нужно уменьшить формат А4, то вы можете превратить его в формат А5, который при повороте будет соответствовать двум копиям, которые идеально поместятся на лист А4 без лишнего пространства. А так как у каждого размера одинаковое соотношение, неважно, насколько вы будете уменьшать или увеличивать, информация на бумаге появится в той же пропорции. Даже в таком обывательском задании, как копирование, геометрия может облегчить нашу жизнь.
Что такое десть?
Понятия, встречающиеся в мире бумаги, очень часто незнакомы обычному человеку. Например, десть – это набор из 24 или 25 листов бумаги одинакового размера, что равно 1/20 стопы (которая равна 400 или 500 листам бумаги).
1.28. Разные варианты изображения Земли на карте
Математические понятия: стереографическая проекция, проекция Меркатора, проекция Робинсона
Если вы когда-нибудь видели карту на чьей-либо стене или дорожный атлас, то вы смотрели на математику в действии. Как вы уже поняли из главы 1.22, когда читали о Гауссе и пицце, невозможно идеально превратить сферическую форму в двухмерную форму. В результате любая карта Земли – или любой другой планеты или сферического тела – будет иметь искажения. Но каким именно образом информацию на шаре превращают в информацию на листе бумаги? Другими словами, как превратить глобус в карту?
Вот здесь в работу вступает математика. Существуют разные виды карт, и каждая из них отображает Землю по-разному. Каждый вид называется проекцией. Вы, возможно, уже слышали о проекции Меркатора (представлена Герардом Меркатором, фламандским картографом, в 1569 году), которая стала отличным помощником морякам, так как, чтобы добраться из точки А в точку Б, штурману надо было всего лишь начертить линию между этими точками, и он знал точное направление по компасу, которое и приводило его в точку назначения. А если вы когда-либо видели настенную карту мира, опубликованную National Geographic, тогда вы знакомы с проекцией Робинсона. (Карты Робисона были спроектированы так, чтобы в приполярных регионах было меньше искажений, а на картах Меркатора они выглядели куда хуже, чем они есть на самом деле.)
Некоторые карты выполнены в форме круга, и центром обычно являются Северный или Южный полюса. Возможно, вы видели древние карты с такой конфигурацией, где были изображены две круглые карты. Такие карты являются стереографической проекцией. В отличие от некоторых карт, стереографические проекции являются конформными, то есть все углы в них приближены к реальности. (Однако этого нельзя сказать о расстоянии и площади.) Кроме того, окружности на глобусе Земли отображаются как окружности на стереографической карте. Если окружности проходят через точку проекции – центр карты, – тогда они отображаются на карте в виде прямых линий.
Проекция Галла – Петерса
В некоторых проекциях, включая проекцию Меркатора, относительные величины континентов искажены. Проекция Галла – Петерса, названная в честь Джеймса Галла и Арно Петерса, пытается скорректировать некоторые искажения, тем самым относительная величина континентов получается более точной. Вы можете помнить знаменитый эпизод «Западного крыла», где эту проекцию поддержала выдуманная Организация картографов за социальное равенство.
1.29. Упаковка M&M’s
Математическое понятие: комбинаторика
Математика может показаться сложной и не связанной с повседневной жизнью, но вы можете столкнуться с ней в самых банальных местах. На самом деле, связь с математикой XVII века можно проследить в отделе сладостей в вашем ближайшем магазине.
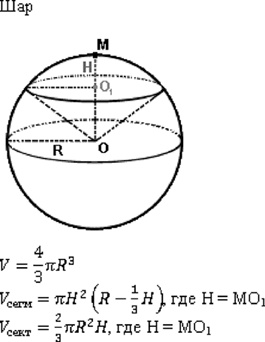
В 1611 году Иоганн Кеплер, который стал известен благодаря открытию законов движения планет (см. главу 1.20), высказал гипотезу, согласно которой, если вы используете частицы в форме шара, то нет лучшего способа заполнить пространство, чем сложить шары так, как складывают апельсины на рынке. (Она еще известна как гипотеза Кеплера.) Используя эту технику, которая называется гранецентрированная кубическая упаковка, человек может заполнить примерно 74 % данного пространства. Если шары заполняют банку бессистемно, то они заполняют примерно 64 % пространства.
Теперь перейдем к конфетам. Исследователи обнаружили, что частицы, которые выглядят как M&M’s – приплюснутые шары или сфероиды, – заполняют сосуд так же, как и шары. Если их сложить как апельсины, то они тоже заполняют примерно 74 % объема. Но если их насыпать в сосуд беспорядочно, то они выигрывают у шаров и заполняют 71 % пространства, а это намного больше, чем у шаров. Некоторые люди считают, что сфероиды эффективнее заполняют пространство, нежели шары, так как они могут переворачиваться, пока не попадут в конфигурацию, которая использует больше пространства. Другие фигуры показывают еще лучший результат. Беспорядочно насыпанные эллипсоиды – похожи на мячи для американского футбола или на миндаль в шоколаде, если вам так больше нравится, – могут заполнить до 74 % объема.
Кеплеру так и не удалось доказать свою гипотезу, однако Гаусс смог предоставить неполное доказательство в 1800-х. Последний шаг в доказательстве был сделан в 1990-х, когда математик Томас Хейлс использовал компьютерную программу, которая и помогла доказать гипотезу. Но доказательство оказалось таким длинным – несколько сотен страниц, – что он воспользовался компьютерным алгоритмом, чтобы проверить его!
Синие M&M’s
В 1995 году ярые любители сладости проголосовали за добавление нового цвета в упаковку M&M’s. Выиграл синий цвет, который набрал 54 % голосов. (Всего было отдано 10 миллионов голосов.) Среди финалистов также были розовый и лиловый цвета.

