Я открыл нечто столь удивительное, что был потрясен, и было бы величайшим несчастьем, если это было бы утеряно. Когда ты, мой дорогой отец, увидишь это, ты все поймешь; сейчас же я могу сказать только одно: я создал странный новый мир из ничего.
Гениальная идея Яноша Бойяи состояла в том, чтобы взглянуть на эту задачу под другим углом. Вместо того чтобы пытаться вывести постулат о параллельности из других аксиом, он позволил своему разуму поставить вопрос так: что если аксиома о параллельных прямых ошибочна? Следует ли из этого противоречие? Янош Бойяи пришел к выводу, что ответ на этот вопрос отрицательный и что существует другая геометрия (не геометрия Евклида, а нечто иное), в которой первые четыре аксиомы верны, а постулат о параллельности – нет. Следовательно, постулат о параллельности не может быть доказан на основании первых четырех аксиом, поскольку такое доказательство исключило бы возможность геометрии Бойяи. Но эта геометрия существует.
Иногда то или иное математические открытие «витает в воздухе»: по едва понятным причинам сообщество ученых готово к очередному достижению, поэтому оно приходит из нескольких источников одновременно. В то время, когда Бойяи в Австро-Венгрии разрабатывал свою неевклидову геометрию, Николай Лобачевский
[304] делал то же самое в России. А великий Карл Фридрих Гаусс, старый друг старшего Бойяи, сформулировал много аналогичных идей в работе, которая до сих пор не опубликована. (Когда Гауссу сообщили о публикации Бойяи, он отреагировал несколько неучтиво: «Хвалить это было бы равносильно тому, чтобы хвалить себя»
{272}.)
Для описания так называемой гиперболической геометрии Бойяи, Лобачевского и Гаусса понадобится намного больше книжного пространства, чем у нас осталось. Однако, как отметил Бернхард Риман несколько десятилетий спустя, существует более простая неевклидова геометрия, которую нельзя назвать безумным новым миром. Речь идет о геометрии сферы.
Давайте вспомним первые четыре аксиомы:
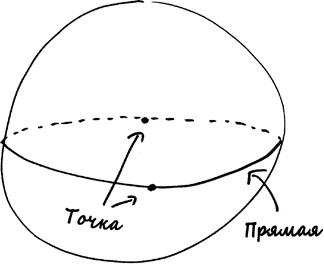
• существует прямая, соединяющая любые две Точки;
• любой отрезок Прямой можно расширить до отрезка Прямой любой требуемой длины;
• для любого отрезка Прямой L есть Окружность с радиусом L;
• все Прямые Углы равны между собой.
Наверное, вы обратили внимание на то, что я внес в описание этих аксиом некоторые изменения, написав термины точка, прямая, окружность и прямой угол с прописной буквы. Я сделал это не ради имитации старинного издания, а чтобы подчеркнуть, что с сугубо логической точки зрения не имеет значения, как обозначены «точки» и «прямые». Мы вольны назвать их лягушками и кумкватами, но структура логического вывода из этих аксиом осталась бы прежней. Это напоминает плоскость Джино Фано из семи точек, на которой «прямые» выглядят совсем не так, как нас учили в школе, однако это не имеет значения: весь смысл в том, что эти прямые ведут себя как прямые согласно законам геометрии. В каком-то смысле было бы даже лучше называть точки лягушками, а прямые кумкватами, поскольку это позволило бы нам избавиться от предвзятого мнения по поводу значений слов Точка и точка, Прямая и прямая.
Вот что означают эти термины в сферической геометрии Римана. Точка – это пара точек на сфере, которые являются антиподальными, или диаметрально противоположными друг другу. Прямая – это большая окружность – другими словами, окружность на поверхности сферы, а отрезок прямой – это отрезок такой окружности. Окружность – это и есть окружность, которая теперь может иметь любой размер.
При таких определениях первые четыре аксиомы Евклида верны! Для любых двух точек (то есть любых двух пар антиподальных точек на сфере) существует прямая (другими словами, большая окружность), которая их соединяет
[305]. Более того (хотя это и не одна из аксиом), любые две прямые пересекаются в одной точке.
У вас могут быть претензии ко второй аксиоме: как мы можем утверждать, что отрезок прямой можно продолжить до любой длины, если он не может быть длиннее самой прямой, которая является окружностью сферы? Это вполне обоснованное возражение, но все сводится к вопросу интерпретации. В понимании Римана в аксиоме идет речь о неограниченных, а не о бесконечно протяженных прямых. Между этими двумя понятиями есть едва уловимое различие: прямые Римана, которые являются окружностями, имеют конечную длину, но они не ограничены, то есть по ним можно передвигаться бесконечно, не останавливаясь.
И наконец пятая аксиома – совсем другая история. Предположим, у нас есть точка Р и прямая L, не содержащая точку P. Есть ли одна и только одна прямая, проходящая через точку Р, параллельная L? Нет, по очень простой причине: в сферической геометрии нет такой штуки, как параллельные прямые! Любые две большие окружности на сфере должны пересекаться.
Доказательство на один абзац. Любая большая окружность С делит сферу на две равные части, каждая из которых имеет одну и ту же площадь; обозначим эту площадь символом А. Теперь допустим, что существует еще одна большая окружность C', параллельная окружности С. Поскольку окружность C' не пересекается с окружностью С, она должна быть полностью расположена с одной или другой стороны С, на одной из полусфер с площадью А. Но это означает, что площадь, ограниченная окружностью C', меньше площади А, что невозможно, поскольку каждая большая окружность ограничивает область, площадь которой равна в точности А.
Следовательно, постулат о параллельности опровергается самым эффектным образом. (В геометрии Бойяи ситуация прямо противоположная. Существует слишком много параллельных прямых: в действительности не просто две, а бесконечное множество прямых проходят через Р параллельно L
[306]. Как вы догадываетесь, такую геометрию трудно визуализировать.)



