Но разве это не окружность? Разумеется, нет! Это правильный многоугольник с 65 536 сторонами! Неужели вы не видите?
Великое озарение Евдокса и Архимеда состоит в том, что на самом деле не имеет значения, что это за фигура – окружность или многоугольник с очень большим количеством очень коротких сторон. Площади этих двух фигур достаточно близки для любых возможных целей. Площадь небольшой области между окружностью и многоугольником была «исчерпана» в процессе нашего неутомимого последовательного приближения. Да, окружность – это кривая, это действительно так. Но каждый крохотный фрагмент этой кривой можно приблизить к идеально прямой линии, подобно тому как крохотный кусочек поверхности Земли, на котором мы стоим, приближен к идеально ровной плоскости
[39].
Следует запомнить девиз: локально прямая, глобально кривая.
Или лучше представьте: вы мчитесь по направлению к окружности с большой высоты; сначала вы видите всю окружность;

затем только один сегмент дуги окружности;

а затем еще более мелкий сегмент.

Продолжайте это до тех пор, пока, приближаясь все больше и больше, вы не увидите нечто напоминающее прямую линию. Ползущему по кругу муравью, видящему лишь пространство, непосредственно его окружающее, представляется, будто он ползет по прямой. Точно так же человеку, стоящему на поверхности Земли, кажется, что он стоит на плоскости (если только он не окажется настолько проницательным, что обратит внимание, как на горизонте поднимаются приближающиеся издалека объекты).
Суть математического анализа, изложенного на одной странице
Теперь я хочу объяснить вам суть математического анализа. Готовы? Вот идея, за которую мы должны благодарить Исаака Ньютона: в идеальном круге нет ничего особенного. Каждая гладкая кривая при достаточном увеличении масштаба напоминает прямую линию
[40]. Не имеет значения, насколько изогнута или закручена эта кривая, – главное, что у нее нет острых углов.
Когда вы запускаете ракету, траектория ее перемещения выглядит так.
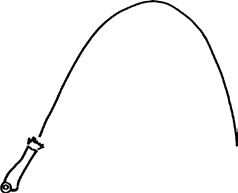
Ракета сначала движется вверх, а затем вниз, образуя параболическую дугу. Сила тяжести изгибает любую траекторию движения по направлению к поверхности Земли; это один из самых фундаментальных законов нашей физической жизни. Но, если мы увеличим масштаб и рассмотрим очень короткий отрезок этой кривой, она будет выглядеть так.

Затем так.

Как и в случае окружности, траектория движения ракеты кажется прямой линией, направленной вверх под определенным углом. Безусловно, эта линия отклоняется под действием силы тяжести, но подобное отклонение слишком незначительно, чтобы увидеть его невооруженным глазом. Приближение к еще более мелкому участку кривой делает линию еще больше похожей на прямую. Чем больше приближение, тем ровнее участок кривой.
А теперь сделаем концептуальный скачок. Ньютон сказал: послушайте, давайте пойдем до конца. Уменьшайте поле зрения до тех пор, пока оно не станет бесконечно малой величиной – настолько малой, что она будет меньше любого размера, который вы можете назвать, но все же не равной нулю. Вы изучаете траекторию движения ракеты не на протяжении очень короткого периода, а в один момент времени. В таком случае то, что было почти прямой линией, становится в точности прямой. Наклон этой кривой Ньютон называл флюксией, а мы называем производной.
Именно этот скачок не был готов совершить Архимед. Он понимал, что многоугольники с более короткими сторонами все более и более приближаются к окружности, но он никогда не говорил о том, что в действительности окружность представляет собой многоугольник с бесконечно большим количеством бесконечно малых сторон.
Некоторые современники Ньютона также не разделяли его точку зрения. Наиболее активно возражал Ньютону Джордж Беркли, который критиковал концепцию бесконечно малых величин Ньютона в крайне издевательском тоне
{23}, как, к сожалению, сейчас уже не пишут в математической литературе:
А что такое эти флюксии? Скорости исчезающих приращений. А что такое эти самые исчезающие приращения? Они не есть ни конечные величины, ни величины бесконечно малые, но они и не нули. Разве мы не имеем права назвать их призраками (ghosts) исчезнувших величин?
[41]








