(1 – p) × 0 = 0
и
p × 1 = p
и получим в итоге p.
Таким образом, ожидаемое количество пересечений – это просто p, то же самое значение, которое вычислил Бюффон. Создается впечатление, что мы так и не продвинулись дальше. Как мы можем найти то загадочное число?
Когда вы сталкиваетесь с математической задачей, которую не знаете, как решить, у вас есть два основных варианта действий. Задачу можно либо упростить, либо сделать сложнее.
Первый вариант кажется более приемлемым: вы используете вместо этой задачи более простую и решаете ее в расчете на то, что понимание, обретенное вами в процессе решения более легкой задачи, поможет вам глубже проникнуть в суть более сложной задачи, которую вы пытаетесь решить. Именно это делают математики каждый раз, когда моделируют сложную реальную систему с помощью отлаженного, безупречного математического механизма. Иногда этот подход применяется весьма успешно: если вы отслеживаете траекторию движения тяжелого реактивного снаряда, вы хорошо справитесь с задачей, не принимая во внимание сопротивление воздуха и считая, что движущееся тело подвержено только постоянному воздействию силы тяжести. В других случаях ваше упрощение достигает такого уровня, что устраняет интересные аспекты задачи, как в старом анекдоте о физике, перед которым поставили задачу оптимизировать процесс производства молочных продуктов, и он без каких-либо сомнений произносит: «Возьмем сферическую корову…»
В этом духе кто-то может попытаться почерпнуть какие-либо идеи в отношении иглы Бюффона посредством решения более простой задачи с игрой франк-карро: «Возьмем круглую иглу…» Однако не совсем понятно, какую полезную информацию можно извлечь из задачи с монетой, чья вращательная симметрия лишает задачу об игле того самого свойства, которое делает ее интересной.
Вместо этого мы используем другую стратегию – стратегию, использованную Барбье: сделаем задачу более сложной. Это звучит не очень обнадеживающе. Но, когда такая стратегия работает, она работает как магическая формула.
Давайте начнем с малого. Что если мы зададим более общий вопрос: чему равно ожидаемое количество пересечений иглы с краями планки, если длина иглы составляет две ширины планки? Это вопрос кажется более сложным, поскольку теперь у нас есть три возможных результата вместо двух. Игла может упасть, полностью расположившись в пределах одной планки, или может пересечь один край планки, или может пересечь два края планки. Следовательно, чтобы вычислить ожидаемое количество пересечений, нам как будто придется вычислить вероятность трех отдельно взятых событий вместо двух.
Однако благодаря аддитивности эта более сложная проблема на самом деле легче, чем вам кажется. Нарисуйте точку посредине длинной иглы и обозначьте две половины цифрами 1 и 2, как на рисунке.
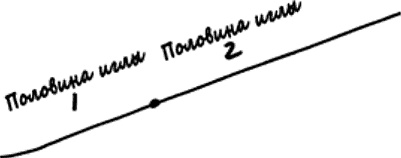
В таком случае ожидаемое количество пересечений длинной иглы равно сумме ожидаемого количества пересечений половины иглы 1 и ожидаемого количества пересечений половины иглы 2. В алгебраических терминах это можно сформулировать так: если Х – это количество краев, пересеченных половиной иглы 1, а Y – количество краев, пересеченных половиной иглы 2, тогда общее количество краев, пересеченных длинной иглой, равно X + Y. Однако каждая половина длинной иглы – это и есть игла той длины, которую изначально рассматривал Бюффон; следовательно, каждая из этих половинок иглы в среднем пересекает края планки p раз. Другими словами, E(X) и E(Y) равны p. Таким образом, ожидаемое количество пересечений целой иглы, E(X+Y), равно сумме E(X) + E(Y), что равно p + p, или 2p.
Такая же логика применима к игле, длина которой в три, в четыре или в сотню раз больше ширины планки. Если длина иглы равна N (а мы теперь берем ширину планки в качестве единицы измерения), ожидаемое количество ее пересечений равно Np.
Такой подход работает как в случае коротких, так и в случае длинных игл. Предположим, я бросаю иглу, длина которой составляет 1/2 единицы, или половину ширины планки. Поскольку иглу Бюффона длиной в 1 единицу можно разделить на две иглы длиной 1/2 единицы, ожидаемая величина p должна быть в два раза больше ожидаемого количества пересечений иглы длиной 1/2 единицы. Следовательно, ожидаемое количество пересечений иглы длиной 1/2 единицы равно (1/2)p. По существу, формула
ожидаемое количество пересечений иглы длиной N = Np
верна для любого положительного действительного числа N, будь то большого или малого.
(Здесь не стоит приводить строгое доказательство того, что представленная выше формула применима и в случае, когда N – некое страшное иррациональное число, скажем квадратный корень из 2, потому что для этого понадобятся формальные математические выкладки. Но я даю честное слово, что основные идеи доказательства Барбье – те, что я привел.)
Теперь необходимо проанализировать задачу под новым, так сказать, углом, согнув иглу.
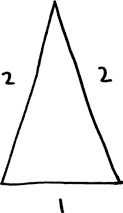
Это самая длинная игла из всех, с которыми мы до сих пор имели дело: ее общая длина равна 5 единицам. Однако эта игла согнута в двух местах, а два ее края я сомкнул, чтобы образовать треугольник. Прямые сегменты иглы имеют длину 1 единица, 2 единицы и 2 единицы; следовательно, ожидаемое количество пересечений каждого сегмента равно p, 2p и 2p соответственно. Количество пересечений всей иглы равно сумме количества пересечений каждого сегмента. Таким образом, принцип аддитивности говорит нам, что ожидаемое количество пересечений целой иглы составляет:
p + 2p + 2p = 5p.
Другими словами, формула
ожидаемое количество пересечений иглы длиной N = Np
применима и в случае согнутых игл.
Вот одна из таких игл.

Вот еще одна.
И еще одна.








