Ситуация «отправился по одному пути, вернулся по другому» поразила молодого Уинстона Черчилля, который дал яркое описание одного математического откровения, произошедшего в его жизни:
Однажды я прочувствовал математику, словно обозрел ее всю, все ее глубины раскрылись передо мной, вся ее бездонность. Подобно тому как многие наблюдают за прохождением Венеры или шествием лорда-мэра, я наблюдал за полетом величины через бесконечность и сменой ее знака с плюса на минус. Я понял, почему это происходит и как один шаг влечет за собой все другие. Похоже на политику. Но озарение пришло после плотного ужина – и мне было не до него!
[217]
По существу, точка R – не просто конечная точка горизонтальной оси, а конечная точка любой горизонтальной линии. Если есть две линии и они обе горизонтальные, значит, это параллельные линии. Тем не менее в проективной геометрии они пересекаются в бесконечно удаленной точке. Дэвиду Фостеру Уоллесу в 1996 году в одном из интервью задали вопрос о концовке романа Infinite Jest («Бесконечная шутка»), который многие считали незавершенным. Журналист поинтересовался у Уоллеса, не уклоняется ли тот от написания заключительной части романа, потому что ему «надоело его писать». Уоллес довольно раздраженно ответил:
Концовка есть, как мне кажется. Считается, что определенные типы параллельных линий начинают сходиться таким образом, что читатель может спроецировать «конец» куда-то за пределы правильной системы координат. Если вы не увидели такого схождения или проекции, значит, книга для вас потеряна
{188}.
* * *
У проективной плоскости есть недостаток: ее трудно нарисовать. Но есть у нее и преимущество, делающее правила геометрии более согласованными. На евклидовой плоскости две различные точки определяют одну прямую, а две различные прямые определяют одну точку пересечения, если только они не параллельные – в таком случае они вообще не пересекаются. В математике мы любим правила, но не любим исключений. С проективной плоскостью вам не придется делать никаких исключений в правиле, говорящем, что две прямые пересекаются в одной точке, поскольку параллельные прямые также пересекаются. Например, любые две вертикальные линии пересекаются в точке Р, а две линии, указывающие с северо-восточного направления в юго-западном, пересекаются в точке Q. Две точки определяют одну линию, две линии пересекаются в одной точке, вот и все
[218]. Здесь имеет место идеальная симметрия, простота и изысканность, не свойственные классической планиметрии. Совсем не случайно, что проективная геометрия возникла естественным образом в результате попыток решить практическую задачу отображения трехмерного мира на плоском холсте. Как раз за разом показывает история науки, математическая элегантность и практическая полезность идут рука об руку. Порой ученые открывают теорию и предоставляют математикам искать объяснение ее элегантности; в других случаях математики разрабатывают элегантную теорию и оставляют ученым искать области ее применения.
Реалистическая живопись – та область деятельности, в которой применяется проективная плоскость. Еще одна такая область – выбор лотерейных номеров.
Миниатюрная геометрия
В основе геометрии проективной плоскости лежат две аксиомы.
Каждая пара точек лежит ровно на одной общей прямой.
Каждая пара прямых линий содержит ровно одну общую точку.
Когда математики обнаружили одну разновидность геометрии, удовлетворявшую этим двум идеально согласованным аксиомам, вполне естественно было задать вопрос, существуют ли другие типы геометрии. Оказывается, есть много таких геометрий, одни большие, а другие маленькие. Самая крохотная из них называется «плоскость Фано», по имени ее создателя Джино Фано, который был одним из первых математиков конца XIX столетия, всерьез воспринявших идею конечных геометрий. Вот как выглядит плоскость Фано.
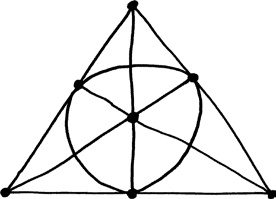
Действительно совсем небольшая геометрическая система, состоящая всего из семи точек! В качестве «прямых» в ней выступают линии, показанные на рисунке; линии также маленькие, поскольку на каждой из них всего по три точки. Существует семь таких линий, шесть из которых выглядят как прямые, а седьмая похожа на окружность. И все-таки эта так называемая геометрия, и без того экзотическая, удовлетворяет и первой и второй аксиомам точно так же, как плоскость Брунеллески.
Фано придерживался современного подхода, достойного восхищения: у него была, говоря словами Харди, «привычка определения», поскольку он избегал вопроса, не имеющего ответа, а именно: «Что такое геометрия?» Вместо этого он спрашивал: «Какой феномен ведет себя подобно геометрии?» Вот свидетельство самого Фано:
A base del nostro studio noi mettiamo una varietà qualsiasi di enti di qualunque natura; enti che chiameremo, per brevità, punti indipendentemente però, ben inteso, dalla loro stessa natura
{189}.
А это перевод:
В качестве основы нашего исследования мы исходим из предположения, что существует произвольная совокупность объектов произвольной природы – объектов, которые мы для краткости называем точками, но это не имеет отношения к их природе
{190}.
Для Фано и его интеллектуальных преемников не имеет значения, «как выглядит» прямая – похожа ли она на линию, на окружность, на крякву или на что угодно. Важно лишь то, что прямые линии подчиняются законам прямых линий – законам, установленным Евклидом и его преемниками. Если это ходит как геометрия и крякает как геометрия, значит, будем называть это геометрией
[219]. Существует точка зрения, согласно которой такой шаг создает разрыв между математикой и реальностью, чему необходимо противостоять. Мнение чрезмерно консервативное. Смелая идея, что мы можем размышлять в геометрических категориях о системах, не похожих на евклидово пространство
[220], и называть эти системы геометриями – причем говорить об этом с высоко поднятой головой, – сыграла решающую роль в осмыслении релятивизма геометрии пространственно-временного континуума, в котором мы живем. В настоящее время мы используем обобщенные геометрические идеи для построения карты интернет-пространства, которое представляет собой нечто весьма далекое от того, что мог представить Евклид. Это один из аспектов красоты математики: мы разрабатываем совокупность идей, и если они верны, то они верны, даже если их применение выходит далеко за рамки контекста, в котором они изначально были задуманы.



