Возьмем в качестве иллюстрации такой пример. На рисунке снова изображена плоскость Фано, но точки на ней обозначены числами от 1 до 7.
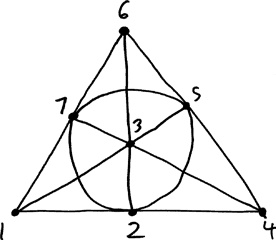
Выглядит знакомо? Если составить список этих семи линий, обозначив их совокупностью трех точек, которые расположены на каждой из них, получится следующее:
124
135
167
257
347
236
456
Это не что иное, как совокупность семи лотерейных билетов, о которых мы говорили выше, – совокупность, в которой каждая пара чисел выпадает только один раз, гарантируя минимальный выигрыш. В тот момент такое свойство казалось впечатляющим и загадочным. Как может кто бы то ни было сформировать столь идеально упорядоченное множество лотерейных билетов?
Ну вот, только что с моей помощью ларчик открылся и продемонстрировал суть фокуса: все дело в геометрии. Каждая пара чисел появляется ровно в одном билете, поскольку каждая пара точек лежит ровно на одной прямой. Это всего лишь Евклид, правда, говорим мы теперь о точках и линиях, и вряд ли Евклид их узнал бы.
Прошу прощения, вы сказали «bofab»?
Плоскость Фано подсказывает нам, как без всякого риска играть в трансильванскую лотерею из семи чисел, но как насчет лотереи штата Массачусетс? Существует множество конечных геометрий с количеством точек, большим семи, но ни одна из них, к сожалению, не отвечает полностью требованиям лотереи Cash WinFall. В этом случае необходимо нечто более универсальное. Решение проблемы проистекает не непосредственно из живописи эпохи Возрождения или евклидовой геометрии, а из еще одного неожиданного источника – теории цифровой обработки сигналов.
Предположим, мне нужно отправить на спутник важное сообщение, например, «Включить правый двигатель». Спутники не разговаривают на человеческом языке, поэтому на самом деле я отправляю последовательность единиц и нулей – то, что программисты называют битами:
1110101…
Сообщение кажется четким и недвусмысленным. Однако в реальной жизни в каналах связи бывают помехи. Может быть, космический луч попадает в спутник в тот момент, когда спутник принимает ваше сообщение, и искажает один бит информации, поэтому в итоге получается такое сообщение:
1010101…
На первый взгляд может показаться, что это сообщение не очень отличается от предыдущего, но, если изменение одного бита информации приведет к замене команды «включить правый двигатель» на команду «включить левый двигатель», у спутника могут возникнуть серьезные проблемы.
Спутники стоят очень дорого, а значит, лучше избегать подобных проблемных ситуаций. Когда вы пытаетесь поговорить с приятелем на бурной вечеринке, то имеете возможность повторить сказанное, и ваши слова не утонут в общем шуме. Данный способ применим и в нашем случае: в исходном сообщении можно продублировать каждый бит, отправив 00 вместо 0 и 11 вместо 1:
11 11 11 00 11 00 11…
Теперь, когда космический луч выбьет второй бит сообщения, спутник увидит такую последовательность:
10 11 11 00 11 00 11…
Спутник знает, что каждый сегмент из двух бит должен представлять собой либо 00, либо 11, а значит, сигнал «10» – признак того, что что-то не в порядке. Но что именно? Спутнику трудно разобраться с этим, поскольку он не знает, в каком именно месте помеха исказила сигнал, не существует способа определить, как выглядело исходное сообщение – 00 или 11.
Но и эту проблему можно исправить, повторив каждый бит три раза вместо двух:
111 111 111 000 111 000 111…
Предположим, сообщение приходит в искаженном виде:
101 111 111 000 111 000 111…
Теперь спутник готов к этому. Он знает, что первый сегмент из трех бит должен представлять собой 000 или 111, а значит, присутствие 101 означает, что что-то пошло не так. Но, если в исходном сообщении была бы последовательность 000, это означало бы, что искажены два бита, расположенные в непосредственной близости друг от друга, – маловероятное событие, учитывая редкость космических лучей, искажающих сообщения. Следовательно, у спутника есть все основания применить принцип большинства: если два из трех бит содержат 1, велика вероятность, что в исходном сообщении была последовательность 111.
Вы только что увидели пример кода с исправлением ошибок – протокол обмена данными, позволяющий получателю устранять ошибки в искаженном сигнале
[221]. Эта идея, как практически и все остальное в теории информации, сформулирована в вышедшей в 1948 году и ставшей сразу классической работе Клода Шеннона Mathematical Theory of Communication («Математическая теория связи»)
[222].
Математическая теория коммуникации! Звучит несколько претенциозно, не так ли? Разве коммуникация – не сугубо человеческий вид деятельности, который нельзя свести к холодным цифрам и формулам?
Я хочу, чтобы вы понимали: я от всей души поддерживаю и настоятельно рекомендую демонстрировать жесткий скептицизм по отношению к любым заявлениям, что ту или иную сущность можно объяснить, или укротить, или полностью понять математическими средствами.
Тем не менее история математики представляет собой историю агрессивной территориальной экспансии, поскольку математические методы становятся все более всеобъемлющими и богатыми, а математики находят способы изучать вопросы, которые раньше считались находящимися вне их области знаний. В наше время словосочетание «математическая теория вероятностей» выглядит вполне обычным, но когда-то могло показаться большим перегибом: математика занималась только изучением определенного и истинного, а не случайного и возможного! Ситуация изменилась, когда Паскаль, Бернулли и другие математики открыли математические законы, описывающие действие случая
[223]. Математическая теория бесконечности? До работы Георга Кантора в XIX столетии изучение бесконечности было не столько наукой, сколько теологией; сейчас мы понимаем теорию Кантора о множественности бесконечностей, каждая из которых бесконечно больше предыдущей, настолько полно, что преподаем эту тему первокурсникам, изучающим математику. (По правде сказать, она действительно поражает их воображение.)



