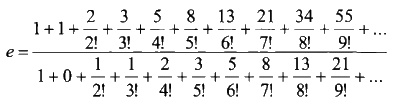И наконец — странное уравнение, объединяющее ряд Фибоначчи с последовательностью факториалов и дающее в пределе значение числа е. Подобно π, это трансцендентное число так и норовит появиться в самых неожиданных местах. Загадочную дробь мне прислал О'Ши, добавив, что нашел ее в Интернете.
Глава 11
Покрытие «изуродованных» шахматных досок с помощью L-тримино
Среди современных математиков приобрела большую популярность так называемая теория покрытий. Нижеследующий текст первоначально был опубликован в «College Mathematical Journal» (май 2009).
Введение
Пусть стандартную шахматную доску «изуродовали», удалив два крайних угловых поля, расположенных по диагонали друг напротив друга. Можно ли оставшиеся 62 квадрата покрыть с помощью 31 прямоугольной костяшки домино? Ответ — нет, потому что убранные квадраты — одного цвета. Допустим, их цвет — белый. Тогда среди оставшихся 62 полей окажутся два «лишних» черных квадрата. Между тем каждая костяшка домино покрывает одну черную и одну белую клетку. После того как мы поместим на доску 30 костяшек, две черные клетки останутся свободными. Они не могут примыкать друг к другу (иметь общую сторону), а следовательно, их невозможно покрыть при помощи костяшек домино. Эта широко известная задача, которая решается элементарной проверкой равенства, являет собой простой пример задачи покрытия изуродованной шахматной доски.
Менее известна связанная с ней другая задача. Предположим, доску изуродовали, удалив две клетки разного цвета из любых мест доски. Всегда ли можно будет покрыть при помощи костяшек домино оставшиеся 62 клетки? Ответ — да, и существует прелестное доказательство, полученное Ральфом Гомори
[72].

Рис. 1. Доказательство Гомори
Проведем по доске жирные линии, как показано на рис. 1. Получим замкнутую дорожку, вдоль которой клетки лежат, словно камешки чередующегося цвета в ожерелье. Если с этой дорожки убрать две любые клетки противоположного цвета, получится два незамкнутых сегмента — или один, если удаленные клетки находились рядом (имели общую сторону).
В каждом сегменте будет поровну черных и белых клеток, а следовательно, его можно будет покрыть с помощью костяшек домино. Остроумное доказательство Гомори легко обобщить, применив его ко всем квадратным доскам с четным числом полей.
Если вместо пластинок домино покрывать доску с помощью L-тримино (называемых также косыми, или V-тримино, или угловыми тримино), тогда все квадратные доски, у которых число клеток без остатка делится на 3, можно будет покрыть такими фигурами (кроме доски 3×3). Среди них мы не будем рассматривать «неповрежденные», а возьмем лишь такие изуродованные доски, где число клеток кратно 3 после того, как из произвольного места доски удалили одну клетку. Будем называть такие доски дефицитными. Иными словами, доска со стороной n является дефицитной, если n2–1 кратно 3; т. е. само n не кратно 3. Длины сторон таких досок образуют ряд (1):
2, 4, 5, 7, 8, 10, 11, 13, 14… (1)
Каждое из этих чисел будем называть порядком доски. И еще: здесь и далее слово «тримино» будет означать исключительно L-тримино.
Основной вопрос: какие дефицитные доски (полученные после того, как из произвольного места обычной доски убрано одно поле) со сторонами из ряда (1) можно покрыть (без разрывов и наложений) с помощью L-тримино? Мы будем рассматривать эти доски, грубо говоря, по возрастанию их порядка, кульминацией же станет полное и универсальное решение задачи.
Степени двойки
Рассмотрим доску второго порядка. Ее можно покрыть, какую бы клетку мы ни удалили (см. рис. 2, слева). На рис. 2, справа, показано, как можно покрыть доску 4-го порядка. Вырезанная клетка неизбежно оказывается в квадрате 2×2, в каком-то из его четырех углов. Остальная часть доски покрывается благодаря приему, который Соломон Голомб окрестил rep-tile («рептилия»): элемент покрытия (tile) как бы воспроизводит увеличенную копию (replica) самого себя. Левый верхний квадрат 2×2 можно поворачивать, чтобы недостающая клетка оказывалась в четырех разных местах, и весь квадрат 4-го порядка можно при этом поворачивать так, чтобы эта клетка попадала на любое из его шестнадцати полей.
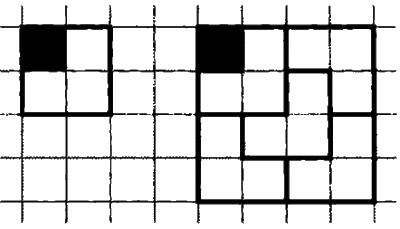
Рис. 2. Порядки 2 и 4
А 1953 году Голомб, «отец» полимино (он придумал для них название и первым начал изучать их), вывел индуктивное доказательство, продемонстрировав, что все доски со сторонами, отвечающими прогрессии 2, 4, 8, 16…) можно покрыть с помощью тримино, когда отсутствует произвольная клетка доски. Впервые доказательство было опубликовано в 1938 году
[73]. Позже его повторил Э.Б. Эскотт (см. статью в журнале «Open Court»
[74]). С тех пор математики включают это доказательство в свои книги, часто без ссылки на Голомба. Роджер Нельсен приводит Голомбово доказательство в виде единственной диаграммы, без всяких словесных пояснений
[75]. Знаменитое доказательство Голомба начинается с рассмотрения квадрата 2×2 (рис. 3, слева). Этот квадрат затем помещается в угол квадрата 4—го порядка (рис. 3, в центре). А уже этот квадрат 4×4 располагается в углу квадрата 8-го порядка (рис. 3, справа), после чего рядом с углом зачерненного квадрата 4-го порядка укладывают одно тримино. Мы уже знаем, что зачерненный квадрат можно покрыть при отсутствии в нем любой клетки, и мы знаем, что три незачерненных области (примыкающих к нашему одиночному тримино) можно покрыть с помощью тримино, так как в каждой из них отсутствует одна клетка (угловая). Поворачивая доску
[76], можно добиться того, чтобы любая клетка в зачерненном квадрате приходилась на любое место доски 8-го порядка.