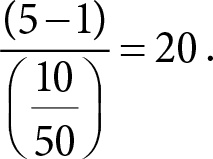Общее количество заходов на сайт, кстати, можно сосчитать и точно, потому что в этом случае не нужно запоминать каждое посещение, достаточно помнить, сколько их было. Число друзей на «Фейсбуке» тоже подсчитывается точно, потому что они не повторяются. Приблизительное решение понадобится для подсчета количества разных объектов, когда один и тот же объект может появиться несколько раз.
Оговоримся, что в примере с кредитными картами проблему можно решить и по-другому, с абсолютной точностью. Например, если выстроить все номера в порядке возрастания, то сосчитать разные номера будет гораздо проще. Очевидный недостаток состоит в том, что обычно к нам поступают неупорядоченные данные и их сортировка представляет собой отдельную, непростую задачу, которой посвящена масса математической литературы.
Еще можно заранее создать такую структуру данных, где на каждого клиента было бы заведено электронное досье. Тогда совсем нетрудно пройтись по всем досье и посчитать, сколько из них содержит трансакции по кредитным картам. К каждому досье понадобится обратиться всего раз, и это много времени не займет. Но данный способ тоже работает не всегда. Например, как посчитать количество магазинов, в которых клиенты воспользовались кредитной картой? Наверняка у банка нет досье на каждый магазин.
Проблема подсчета очень актуальна, особенно в контексте больших данных. Сколько посетителей заходит на наш сайт из разных регионов России? Сколько школьников в этом году подали заявления в вузы? Сколько людей обсуждают в социальных сетях нашу партию? Сотрудники Google в своей статье
{20}
пишут, что в их систему хранения и обработки данных поступает свыше пяти миллионов подобных запросов в день! Регулярно встречаются запросы, предполагающие подсчет более миллиарда объектов. В этой статье также приводится цифра: в среднем около ста таких запросов в день. Из-за ограничений памяти получить точный ответ на подобный запрос абсолютно нереально.
Как найти хорошее приближение, практически ничего не запоминая? У задачи подсчета есть несколько решений. Сходу такое решение нельзя придумать, но понять основные идеи не так уж сложно.
Как решается задача подсчета
Мы воспользуемся блестящим блогом
{21}
и начнем с метода К-Minimum Values [K-минимальные величины]. Идея очень проста. Допустим, значения, которые надо посчитать, равномерно разбросаны в каком-то интервале. В нашем примере с номерами карточек от 01 до 50 и их непредсказуемым использованием это предположение вполне разумно. Теперь давайте не будем запоминать все увиденные значения, а запомним лишь несколько самых маленьких.
Возьмем снова пример с кредитными картами, где трансакций было 30, а разных карт – 22. Мы можем запомнить, скажем, всего пять самых маленьких значений. В данном случае это номера 01, 02, 05, 08 и 10. Пять значений в интервале от 1 до 10. Значит, сколько разных значений мы встретим в интервале от 1 до 50? Интервал в пять раз длиннее, значения разбросаны равномерно. Стало быть, всего значений будет
5 (значений) × 5 (интервалов) = 25 (значений)
примерно двадцать пять. Поскольку число 10 находится на самой границе интервала, делается коррекция. Для большей точности в данном случае пользуются формулой
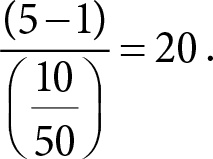
Это, конечно, не равняется точному ответу 22, но достаточно близко к нему. При этом нам пришлось запомнить только 5 значений, а не 22.
Хранить в оперативной памяти всего несколько самых маленьких значений уже вполне реально, но по-прежнему не идеально. Чем больше значений мы сохраняем, тем выше точность, и для действительно высокой точности значений нужно хранить довольно много.
Можно ли сделать лучше? Оказывается, можно. Настоящую революцию в мире счетчиков совершил французский математик Филипп Флажоле. Его результаты были опубликованы в 2007 году в статье
{22}
, а сейчас широко применяются в системах обработки данных, в том числе BigQuery Google и Redis компании Amazon.
HyperLogLog-счетчики
Филипп Флажоле и соавторы предложили новый метод подсчета под названием HyperLogLog.
LogLog означает, что по сравнению с числом объектов нам нужно очень маленькое количество оперативной памяти. Под LogLog здесь понимают двойной логарифм по основанию 2, и это на самом деле очень маленькое число. Например, при миллиарде объектов двойной логарифм будет
log2(log2(1000 000 000)) ≈ 4,9,
то есть порядка 5 битов памяти – всего пять нулей и единиц!
Приставка Hyper использована тоже не просто так. Идею подобного метода Флажоле предлагал и раньше, но предыдущие версии давали слишком грубые результаты.
Метод HyperLogLog сильно улучшил точность, что позволило применить его на практике.
Как и в методе К-Minimum Values, Флажоле исходил из предположения, что записи в базе данных можно представить в виде разбросанных случайным образом чисел. На практике это действительно так, потому что каждой записи, будь то число, имя, адрес или название, присваивается так называемое хеш-значение. Это последовательность из нулей и единиц одинаковой небольшой длины. Если две записи совпадают (например, одно и то же название повторяется два раза), то и их хеш-значения совпадают. Например, хеш-значения длины 8 для разных веб-магазинов могут выглядеть примерно как в табл. 7.1. Мы выделили жирным шрифтом название, которое повторяется два раза:
Таблица 7.1. Фиктивный пример хеш-значений веб-магазинов