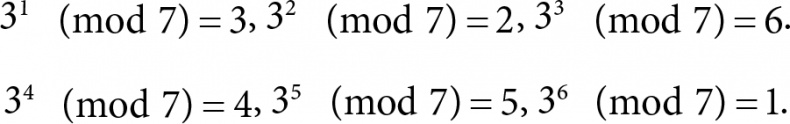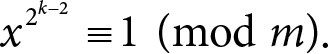Одна нетривиальная теорема из теории чисел (см., например,
{35}
) утверждает, что для каждого простого р существует такое число g, что все числа

разные, то есть служат перестановкой множества 1, 2, …, p − 1 (среди них нет нуля, поскольку g < p и, значит, gх не делится на р). Например,
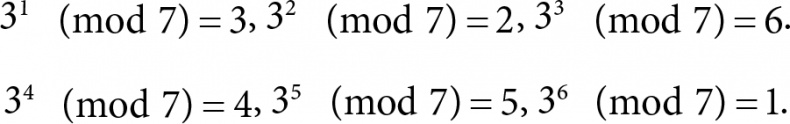
Из этого следует возможность корректного определения дискретного логарифма, который еще называется индексом. А именно: «логарифм» произвольного числа y ∈ {1, 2, …, p − 1} по основанию g – это тот самый, уникальный, x ∈ {1, 2, …, p − 1}, при котором выполняется gx (mod p) = y. Поскольку для всех x < p остатки разные, то х определяется однозначно. Операция нахождения такого х называется операцией дискретного логарифмирования. Она очень сложная, и никто не знает, можно ли придумать способ ее быстрой реализации.
Как определить такое число g, чтобы все остатки в выражении (П.15) были разные? Число g обладает этим свойством, если оно является первообразным корнем числа р. Мы позволим себе рассказать об этом понятии немножко подробнее.
3. Первообразные корни
Есть такая теорема Эйлера: если х и m взаимно просты, то gφ(m) ≡ 1. Здесь a ≡ b, если a − b делится на m. Другими словами, у а и b одинаковый остаток от деления на m. А φ(m) это функция Эйлера, равная количеству чисел, не превосходящих m и взаимно простых с ним. Например, если m = p, где р простое, то φ(p) = p − 1 и теорема Эйлера превращается в малую теорему Ферма.
Условие теоремы Эйлера достаточное, но не необходимое. Вполне может случиться и так, что xa ≡ 1 (mod m), хотя a < φ(m). Самый простой пример такой ситуации – это, конечно, x = 1. Действительно, xa ≡ 1 (mod m) для любых натуральных a и m. Но есть и менее тривиальные примеры. Скажем, p = 5, а 4² = 16 ≡ 1(mod 5), хотя 2 < p − 1 = 4.
Формально число g называется первообразным корнем по модулю m, если
gφ(m) ≡ 1 (mod m), но ga ≢ 1 (mod m) при всех a < φ(m) и a ≠ 0.
Пример (отсутствие первообразных корней у m = 2k). Возьмем m = 2k при k ≥ 3. В этом случае можно показать, что для любого натурального х выполняется
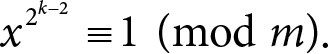
При этом φ(m) = 2k−1, потому что числа, взаимно простые со степенью двойки, – это все нечетные числа, а их ровно 2k−1. Значит, для любого х нашлось число
a = 2k−2 < 2k−1 = φ(m),
для которого выполняется xa ≡ 1 (mod m). Получается, что у m = 2k при k ≥ 3 первообразных корней нет.
Теперь мы можем объяснить, почему в качестве m удобно брать простое число р. Для простого р всегда существуют первообразные корни. На самом деле мы уже говорили о них выше, в
приложении 2 к главе 6
, только не называли этим термином. Это те самые числа g, которые дают разные остатки от деления на p в (П.15). Например, при p = 3 это g = 2, при p = 5 это g = 2, а при p = 7 это g = 3. В нашем примере в тексте главы число g = 2 – это один из первообразных корней числа p = 19.
Итак, если g – первообразный корень p, то все остатки в (П.15) разные и каждому остатку соответствует единственная степень х (дискретный логарифм, он же индекс), при которой такой остаток получается. Ничего подобного мы не можем сделать, если будем брать остаток от деления на число m, для которого первообразного корня нет. Именно поэтому работают с простыми числами.
Заметим, что первообразные корни есть еще для m = 4, m = pk и m = 2pk. Но все равно с простыми числами работать проще.
Назад к Главе 6
Приложение к главе 7
Двойной логарифм в HyperLogLog
Хеш-значения – это последовательности из нулей и единиц одинаковой длины. Обозначим длину хеш-значений через т. Тогда получим 2m разных хеш-значений (см. главу 3
и
приложение 1
к ней).
Теперь допустим, что нам нужно сосчитать n различных объектов. Чтобы присвоить им всем разные хеш-значения, понадобится как минимум n хеш-значений, то есть
Стало быть, m должно быть того же порядка величины, что и log2(n).
Алгоритм К-Minimum Values запоминает К самых маленьких хеш-значений длины m, то есть для этого алгоритма нам нужен объем памяти примерно K log2(n).
HyperLogLog запоминает только максимальное количество нулей в начале хеш-значений. Если сами хеш-значения длины m, то и нулей может быть не больше, чем т. Значит, нам нужно держать в памяти число между 0 и m. Оно тоже записывается с помощью последовательности нулей и единиц. Какой длины должны быть эти последовательности? Если последовательности длины l, то мы можем записать 2l разных чисел. Стало быть, чтобы записать m + 1 разных чисел, должно выполняться