0 ≤ АЮ ≤ 60,
0 ≤ БЮ ≤ 40,
АЮ + БЮ ≤ 70,
АЮ + БЮ ≥ 65.
Мы добавили, что АЮ и БЮ либо ноль, либо больше нуля, потому что доставить клиенту отрицательное количество листов железа невозможно.
Программирование в данном контексте скорее «оптимизация», а не программирование на компьютере. Слово линейное употребляется потому, что используются исключительно линейные выражения, то есть переменные можно умножать на число, а также вычитать и складывать. И все. Никакие другие операции не применяются. Например, у нас нет выражений типа АЮ × БЮ или АЮ². Оказывается, в такой линейной формулировке можно представить очень многие задачи оптимизации.
В практических задачах переменных и ограничений намного больше. При этом всегда есть только одно выражение, так называемая целевая функция, которую следует либо минимизировать (если речь идет о стоимости), либо максимизировать (если речь идет о доходе). В данном случае наша целевая функция – стоимость (2.1), и ее нужно минимизировать.
Теория для практики
Пионер и основатель теории линейного программирования – советский ученый Леонид Витальевич Канторович. Над подобными проблемами он работал в конце 1930-х годов. В 1940-м вышла его фундаментальная статья «Об одном эффективном методе решения некоторых классов экстремальных проблем»
{2}
. В ней Канторович заложил математические основы линейного программирования (правда, тогда оно еще так не называлось).
Канторович интересовался этими проблемами прежде всего из-за их практической ценности. В 1975 году он получил Нобелевскую премию «за вклад в теорию оптимального распределения ресурсов», которую разделил с американским экономистом-математиком голландского происхождения Тьяллингом Купмансом, тоже занимавшимся разработкой теории линейного программирования и ее приложениями в экономике.
Одна из классических знаменитых задач линейного программирования – задача о диете Стиглера, датируемая 1945 годом. Звучит она примерно так: какие из 77 продуктов должны входить в потребительскую корзину одного человека (скажем, мужчины среднего веса), чтобы он получил необходимую норму девяти питательных веществ (включая калории) и при этом стоимость продуктов была минимальной? Это очень важная задача в экономике, потому что ее решение определяет минимальную потребительскую стоимость полноценного питания.
В математической формулировке переменные – это количество каждого продукта. Содержание белков, жиров, витаминов, минералов в каждом продукте известно. Ограничения – это минимальное количество питательных веществ. А минимизировать надо общую стоимость продуктов, которая складывается из количества каждого продукта, помноженного на его цену.
Уже к концу 1950-х линейное программирование достаточно широко использовалось в нефтяной индустрии. Сегодня оно лежит в основе огромного класса задач оптимизации, включая задачи менеджмента и микроэкономики: планирование, логистика, составление расписаний. Задачи, где нужно минимизировать стоимость или максимизировать доход при заданных ограничениях.
От задачи к решению
Несмотря на простую формулировку, решить задачу линейного программирования вовсе не просто. Самая большая сложность заключается в ограничениях. Это видно даже на нашем маленьком примере. Понятно, что выгоднее всего доставить товар обоим клиентам с дешевого южного склада. Трудность в том, что это невозможно, потому что там всего 70 листов, а нам нужно 100.
Чем больше переменных и ограничений, тем сложнее задача. В классической задаче о диете 77 переменных и 9 ограничений, и она уже представляет собой серьезную проблему с точки зрения вычислений. Линейное программирование стало рядовым инструментом менеджмента и планирования только благодаря тому, что математики придумали для таких задач множество совершенно нетривиальных методов решения.
Работы американского математика Джорджа Данцига появились в конце 1940-х годов – несколько позже, чем работы Канторовича. Тем не менее Данцига тоже по праву относят к основателям линейного программирования. Именно он придумал так называемый симплекс-метод, позволивший с помощью компьютера быстро решать задачи линейного программирования с большим количеством переменных и ограничений.
Симплекс-метод, сильно улучшенный и усиленный другими методами, по-прежнему остается неотъемлемой частью современного программного обеспечения.
Идея симплекс-метода
Подробности симплекс-метода выходят за рамки этой книги, но мы постараемся объяснить его суть на нашем маленьком примере.
Для начала давайте посмотрим, какие в принципе значения могут принимать переменные, чтобы не нарушить наших ограничений. Например, мы можем взять АЮ = 58, БЮ = 8. В этом случае получается решение, которое мы записали в виде табл. 2.2.
Таблица 2.2. Пример решения, где АЮ = 58, БЮ = 8

Ограничения выполнены, и оба клиента получили заказанное количество листов.
Но это не единственное решение. Например, мы могли отправить больше листов с дешевого южного склада клиенту А, скажем 60 листов, и 10 листов клиенту Б. Легко увидеть, что доставка клиенту А теперь обойдется в
5×60=300 руб.,
а доставка клиенту Б будет стоить
10×10+30×15=550 руб.
Тогда общая стоимость получается не 864, а 850 рублей, то есть немного меньше, чем указано в табл. 2.2.
Чтобы не выбирать наугад, нужно посмотреть на все возможные решения, которые удовлетворяют ограничениям. Мы их изобразили на рис. 2.1. По оси х мы откладываем АЮ, а по оси у – БЮ. Любая точка в заштрихованной области удовлетворяет ограничениям. В том числе точка (58,8), как в таблице выше.
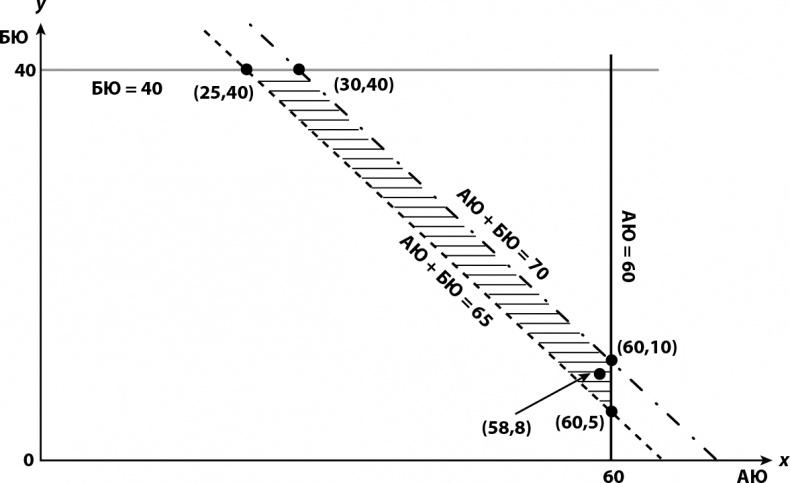
Рис. 2.1. Решения, удовлетворяющие ограничениям
Примечание: любая точка в заштрихованной области удовлетворяет всем ограничениям. Точка (58,8) это решение из таблицы выше. Угловые точки (25,40), (30,40), (60,10) и (60,5) кандидаты на оптимальное решение (см. объяснение в тексте).
Ниже во врезке мы объясняем, как получилась заштрихованная область. Объяснения соответствуют уровню средней школы. При желании их можно пропустить.




