Отклонения от среднего по обеим величинам у первых, зажиточных котиков будут положительными числами, а у вторых — отрицательными. Однако если вы возьмете любого из них (назовем его Барсиком) и перемножите его отклонения между собой, то вы получите положительное число. В том числе и потому, что минус на минус дает плюс.
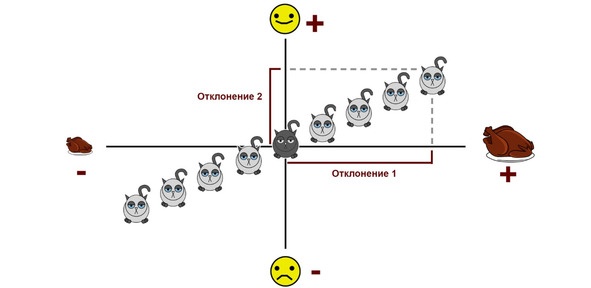
Теперь представим обратную ситуацию: чем больше порции, тем менее счастливыми становятся котики (типичного представителя этой группы мы назовем Мурзиком). В этом случае мы также наблюдаем разделение на две группы: несчастных обжор и счастливых голодающих. Но и у тех, и у других знак одного отклонения будет положительным, а знак другого — отрицательным. А как мы знаем, произведение положительного и отрицательного чисел дает отрицательное число.
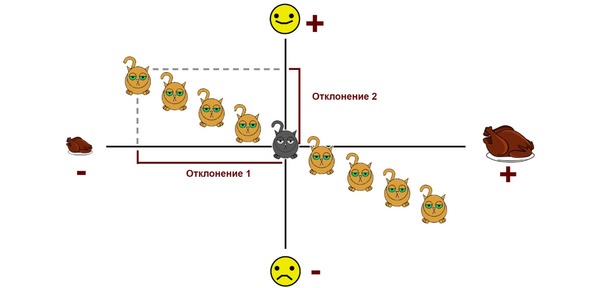
Иными словами, знак, который получается при перемножении отклонений, может служить индикатором того, является ли наш котик Барсиком, который становится счастливее при увеличении порций, либо Мурзиком, которому еда отвратительна. Осталось только понять, кто из них делает больший вклад в наблюдаемые данные, что достигается простым суммированием полученных произведений. Если при результате стоит плюс, то победили Барсики и связь положительная. Если минус — то преобладают Мурзики и связь отрицательная. Если же ответ близок к нулю, объявляется боевая ничья и признается отсутствие связи.
Далее с помощью некоторых нехитрых преобразований этот результат приводят в нужную размерность, получив так называемый коэффициент корреляции Пирсона. Он может изменяться в пределах от -1 до 1, где -1 — отрицательная связь, +1 — положительная связь, а 0 — отсутствие всякой связи.
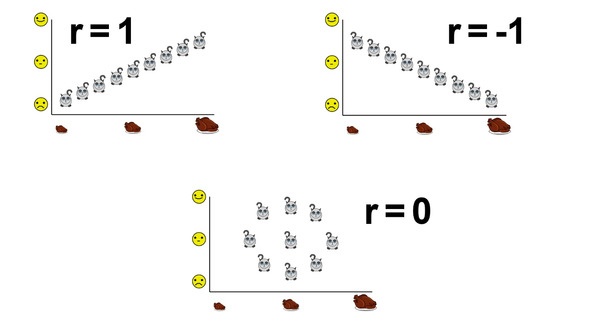
Нулевая гипотеза такого коэффициента — связи нет, альтернативная — связь есть (не важно, положительная или отрицательная). Если коэффициент корреляции достаточно большой по модулю, то нулевая гипотеза отвергается в пользу альтернативной.
Основная проблема r Пирсона как параметрического критерия (т. е. использующего в расчетной формуле средние значения) заключается в том, что он очень не любит выбросы и ненормальные распределения. Поэтому у него есть непараметрический аналог — коэффициент корреляции Спирмена.
Чтобы его вычислить, упорядочим наших котиков от самого счастливого до самого несчастного и присвоим им ранги. Затем мы перераспределим их от самого переедающего до самого голодного и присвоим им ранги уже по этому признаку. Если результаты обоих ранжирований будут совпадать между собой, то мы можем констатировать положительную связь, если же они будут диаметрально противоположными — отрицательную.

Критерий Спирмена мы получаем, применив специальную формулу к нашим рангам, и он интерпретируется аналогично r-критерию Пирсона.
Как правило, проводя корреляционный анализ, мы анализируем сразу несколько переменных и по итогу получаем так называемую корреляционную матрицу. В ней записаны все вычисленные коэффициенты корреляции. Чтобы найти, какие переменные связаны с счастьем, достаточно найти нужный столбик и посмотреть, какие из этих коэффициентов являются значимыми.
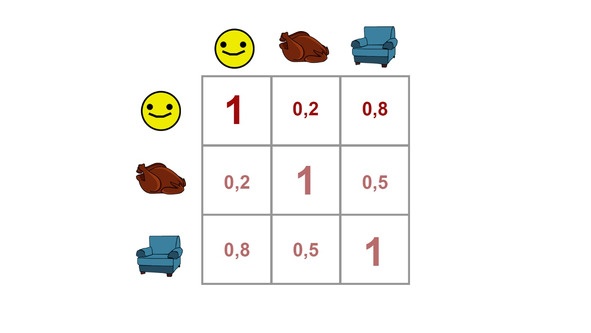
Единственное — если вы находите несколько коэффициентов корреляции одновременно, то здесь опять возникает проблема множественных сравнений. Решить ее можно, применив всю ту же поправку Бонферрони: поделив критический p-уровень значимости (0,05) на количество вычисленных критериев (в нашем случае на 3) и сравнив наш p-уровень с получившимся значением (0,017).
К большому сожалению, корреляционный анализ позволяет установить только само наличие связи. Однако сказать, насколько сильно тот или иной фактор влияет на счастье, он не способен. Для этого используются более мощные методы, о которых мы поговорим в следующей главе.
НЕМАЛОВАЖНО ЗНАТЬ!
Корреляция может обмануть
При проведении корреляционного анализа очень важно помнить, что высокий коэффициент корреляции не всегда указывает на характер связи между явлениями. В качестве примера предположим, что мы нашли взаимосвязь между размером котиков и их эмоциональным состоянием. Иными словами — чем больше котик, тем он счастливее.
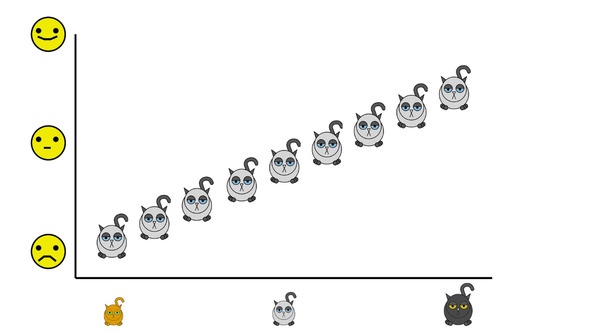
Тогда теоретически равноправными являются следующие утверждения.
1. Большие котики лучше реализуются в жизни и от того более счастливы.
2. Хорошее расположение духа вызывает более активную выработку гормонов роста, что и приводит к данному эффекту.
3. Существует некоторая третья переменная, которая обусловливает как хорошее настроение, так и разницу в размерах. Например, качество и количество котикового корма.
4. Это просто совпадение.
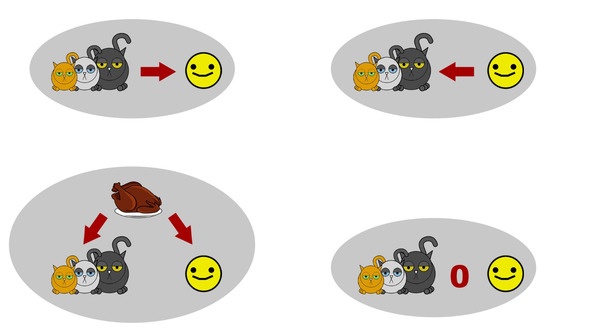
И чтобы определить, какая из этих гипотез верна, необходимо организовать экспериментальное исследование, о котором шла речь в предыдущих главах.
Глава 10.
Формула счастья
или основы регрессионного анализа
Из предыдущей главы вы узнали, как определить, что делает наших котиков счастливыми. Для этих целей мы использовали корреляционный анализ. Однако коэффициенты корреляции позволяют установить лишь само наличие и выяснить направление этой связи. Определить, насколько сильно изменяется одна переменная под воздействием другой, он не в силах. В качестве иллюстрации приведем пример.
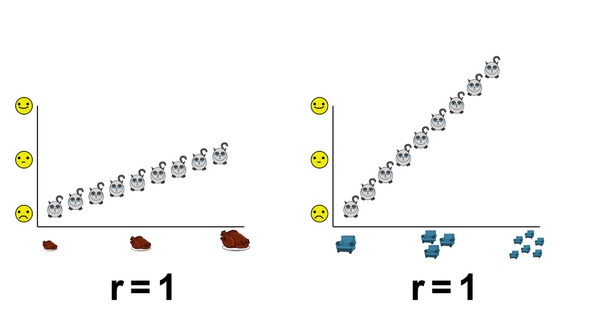
На графиках изображены две линейные положительные взаимосвязи. Коэффициент корреляции в обоих случаях равен +1. Однако очевидно, что каждый подранный диван делает котиков гораздо счастливее, чем очередное увеличение пайков. Эта разница математически описывается с помощью коэффициента b1. Он определяется как тангенс угла между линией котиков и горизонтальной оси x. Чем больше этот коэффициент, тем сильнее растет уровень счастья от каждой новой порции.

