Дисперсионный анализ хорош тем, что позволяет сравнивать между собой любое количество групп (две, три, четыре и т. д.) Его нулевая гипотеза состоит в том, что животные абсолютно не различаются между собой по размеру. Альтернативная гипотеза — хотя бы один вид значимо отличается от остальных.
Теперь посмотрим, как это работает.
Во-первых, давайте объединим котиков, песиков и слоников вместе и отметим их общее разнообразие. Мы можем заметить, что размеры их типичных представителей могут существенно различаться. Например, средний слоник намного больше среднего котика.
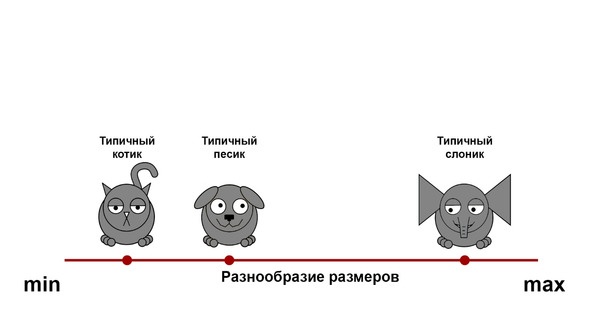
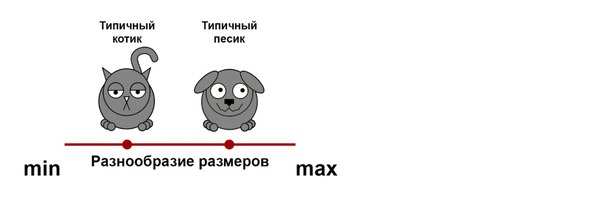
Теперь предположим, что мы убрали отсюда всех слоников. Как вы можете заметить, разнообразие размеров сильно уменьшилось, поскольку слоники вносили в него существенный вклад. И чем сильнее типичные слоники отличались от остальных, тем больше был этот вклад.
Однако отметим, что котики, песики и слоники по отдельности также бывают весьма различными в зависимости от возраста, генов и режима питания. Теоретически мы можем встретить как очень большого котика, так и весьма маленького слоника.
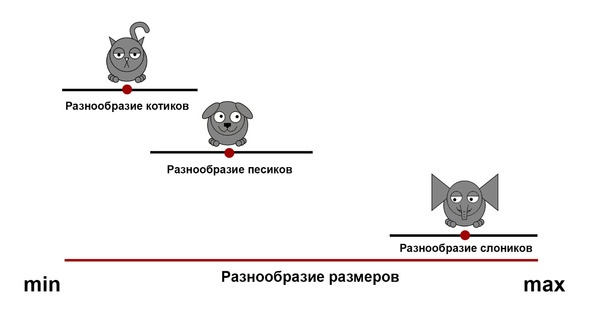
Таким образом, разнообразие размеров складывается как из принадлежности животного к тому или иному виду, так и из абсолютно «левых» факторов. И наша задача — сравнить между собой их вклады.
Как мы помним, одной из основных мер, определяющих разнообразие, является дисперсия. И дисперсионный анализ работает именно с ней. Он выделяет ту часть дисперсии, которая обусловлена фактором вида (межгрупповую дисперсию), и ту, которая определяется прочими факторами (внутригрупповую дисперсию), а затем сравнивает их по F-критерию Фишера, с которым мы встречались раньше. И чем больше будет значение этого критерия, тем сильнее фактор вида влияет на размер животных.

К большому сожалению, дисперсионный анализ является параметрическим методом, а следовательно, не очень любит выбросы и ненормальные распределения данных. Если у вас такая ситуация, то рекомендуется воспользоваться его непараметрическим кузеном — H-критерием Краскела-Уоллеса. Последний очень похож на критерий Манна-Уитни, который мы рассматривали в одном из предыдущих разделов.
Мы точно так же объединяем всех животных в одну группу, упорядочиваем их от самого большого до самого маленького и присваиваем им ранги.
Затем они снова делятся на группы, ранги внутри групп складываются, и их суммы сравниваются между собой. Логика здесь такая: чем сильнее различаются суммы рангов, тем больше вероятность отвергнуть нулевую гипотезу. И коэффициент Краскела-Уоллеса как раз и отражает различия в этих суммах.
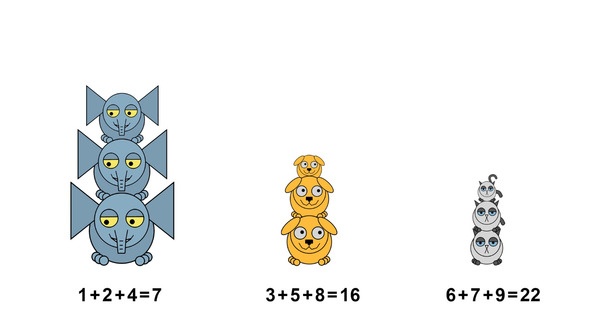
В заключение напомним, что после вычисления любого из этих критериев необходимо найти соответствующий им p-уровень значимости. Именно он и покажет, существует ли связь между размерами и биологическим видом.
НЕМАЛОВАЖНО ЗНАТЬ!
Проблема множественных сравнений
К большому сожалению, если мы получили значимые результаты по дисперсионному анализу, мы не сможем по ним сказать, кто от кого отличается по размеру: слоники от котиков или песики от слоников. Мало того — мы не можем просто взять и сравнить их попарно с помощью t-критерия Стьюдента. Истоки этого — в основах теории вероятности, и мы не будем на них подробно останавливаться. Просто отметим, что с каждым таким сравнением вы серьезно увеличиваете свои шансы ошибиться в выводах. Эта неприятная вещь называется проблемой множественных сравнений.
Поэтому такие сравнения необходимо проводить с помощью других, так называемых апостериорных критериев (или критериев post hoc).
Простейший из них называется t-критерием Стьюдента с поправкой Бонферрони. Вычисляется он как самый обычный t Стьюдента. Поправка же касается критического значения, с которым мы сравниваем p-уровень значимости (0,05). Это значение нужно поделить на количество попарных сравнений.
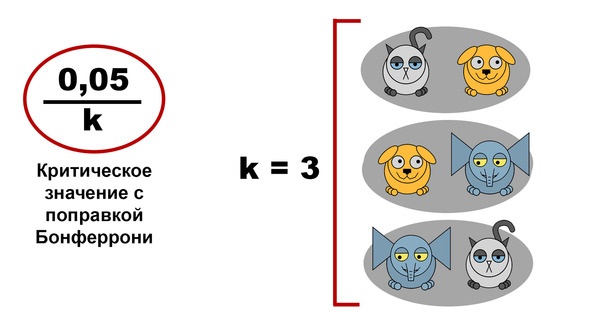
Если вы сравниваете три вида животных, то таких сравнений тоже будет три (котики с песиками, песики со слониками и слоники с котиками). А вот если их четыре, то количество сравнений увеличивается до шести. И тогда критическое значение будет равно 0,05 / 6.
Применив поправку Бонферрони, посмотрите на ваш p-уровень значимости. Если он ниже получившегося значения, то песики и котики различаются, если же нет, то нет.

Помимо t-критерия Стьюдента с поправкой Бонферрони существует еще, по крайней мере, 17 апостериорных критериев, которые применяются в различных ситуациях. В первом приближении мы можем разбить их на две группы. В первую входят те критерии, которые применяются, если дисперсии котиков, песиков и слоников не отличаются друг от друга, а вот вторая группа содержит критерии для случая неравных дисперсий. Самые популярные из них представлены ниже.

Глава 6.
Диета для котиков
или многофакторный дисперсионный анализ
Из предыдущей главы мы узнали, как определить взаимосвязь между биологическим видом животного и его размером с помощью дисперсионного анализа. Однако, помимо вида, на размер могут повлиять и другие факторы, например, питание.
При этом на котиков, песиков и слоников оно может влиять по-разному. Так, мясная диета будет очень нравиться котикам и песикам, в то время как слоники от нее загрустят и будут голодать.

