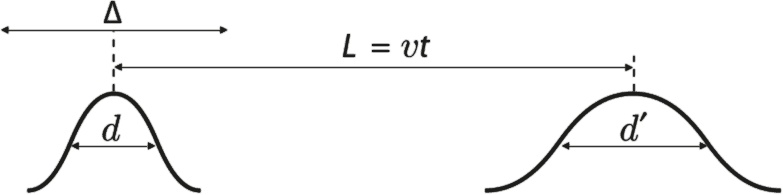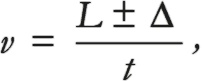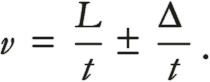Мы рисовали эту ситуацию на рис. 5.3, обозначив исходную ширину волнового пакета d и разрешение нашего детектора Δ.
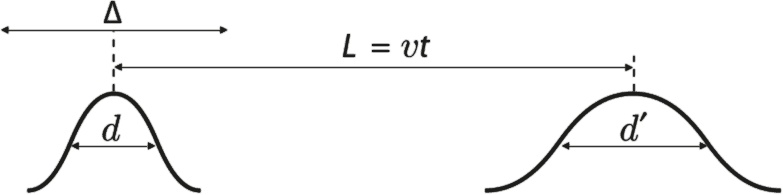
Рис. 5.3. Волновой пакет в два разных момента времени. Пакет двигается вправо и распространяется с течением времени. Пакет движется, потому что стрелки часов, которые его составляют, смещены относительно друг друга (де Бройль), и распространяется в соответствии с принципом неопределенности. Форма волнового пакета не так важна, но для полноты картины следует сказать, что если пакет большой, то циферблаты будут большими, а если пакет маленький, то небольшими будут и циферблаты
Мы изобразили также волновой пакет в более позднее время: он стал немного шире и имеет ширину d', которая больше, чем d. Максимум волнового пакета проходит расстояние L за временной интервал t со скоростью v. Приносим извинения, если эта формула навеяла вам давно забытые школьные дни, бездарно просиженные за исчерканной и покореженной деревянной партой, и голос учителя физики, теряющийся в полумраке зимнего дня и вгоняющий в совершенно неуместную дремоту. Мы покрываемся тут меловой пылью по серьезной причине и надеемся, что заключение этой главы вернет вас в сознание эффективнее, чем летающая тряпка для вытирания доски в детстве.
Снова оказавшись в нашей метафорической научной лаборатории, мы пытаемся измерить скорость v волнового пакета, выполнив два измерения его положения в два разных мгновения. Это даст нам расстояние L, которое волновой пакет покрыл за время t. Но разрешение нашего детектора равно Δ, так что мы не сможем точно вычислить L. В символической форме можно записать, что измеренная скорость равна
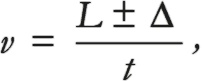
где знак плюс-минус просто напоминает, что если мы проводим два измерения положения, то получаем обычно не L, а скорее «L плюс чуть-чуть» или «L минус чуть-чуть», где «чуть-чуть» получается благодаря тому, что мы согласились не измерять положение частицы слишком точно. Важно принять во внимание, что L мы в действительности измерить не можем: мы всегда получаем значение где-то в диапазоне L ± Δ. Помните также, что величина Δ должна быть гораздо больше, чем размер волнового пакета, иначе частица сожмется и разрушит его. Немного перепишем последнее уравнение, чтобы лучше понять, что происходит:
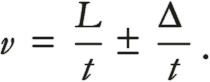
Оказывается, что, если величина t будет очень большой, мы выполним измерение скорости v = L / t с весьма незначительной погрешностью, потому что можем ждать очень долго, добиться, чтобы t было сколь угодно большим, а Δ / t, соответственно, сколь угодно малым, притом что величина Δ продолжит оставаться достаточно великой. Поэтому кажется, что мы нашли отличный способ все же совершить точные вычисления скорости этой частицы, не вмешиваясь в ее ход: достаточно лишь долго подождать между первым и вторым измерениями. С точки зрения интуиции все прекрасно и логично. Представьте, что вы замеряете скорость автомобиля, движущегося по шоссе. Если замерите расстояние, которое он проедет за одну минуту, то вы, конечно, получите значительно более точный показатель его скорости, чем если интервал между измерениями составит одну секунду. Итак, мы обманули Гейзенберга?
Конечно, нет: мы забыли кое-что учесть. Частица описывается волновым пакетом, который рассеивается с течением времени. При наличии достаточного времени рассеяние окончательно размоет волновой пакет, так что частица может оказаться где угодно. Это увеличит диапазон значений, которые мы получим при измерении L, и перекроет нам возможность совершать сколь угодно точное вычисление скорости частицы.
Имея дело с частицей, описываемой волновым пакетом, мы все равно ограничены принципом неопределенности. Так как изначально частица находится где-то в области размером d, Гейзенберг информирует нас, что импульс частицы соответствующим образом искажается на величину h/d. Поэтому есть только один способ построения такой конфигурации циферблатов, чтобы представленная на ней частица двигалась с определенным импульсом, – нужно сделать d, то есть размер волнового пакета, очень большим. И чем больше он будет, тем меньше окажется неопределенность импульса частицы. Урок ясен: частица с хорошо известным импульсом описывается большой группой циферблатов
[17]. Точнее говоря, частица с совершенно точно известным импульсом будет описана бесконечно длинной группой циферблатов, что означает бесконечно длинный волновой пакет.
Мы только что показали, что волновому пакету конечного размера не соответствует частица с определенным импульсом. Это значит, что, если измерить импульс очень большого количества частиц, которые описываются одним и тем же исходным волновым пакетом, мы не получим каждый раз один и тот же результат. Напротив, мы получим широкий набор разных ответов, и их разброс, как бы хороши мы ни были в экспериментальной физике, не может оказаться меньше, чем h / d.
Таким образом, мы можем сказать, что волновой пакет описывает частицу, которая движется с импульсом, определенным в рамках некоторого диапазона. Но уравнение де Бройля подразумевает, что в последнем предложении можно заменить слово «импульсы» словами «длины волн», потому что импульс частицы связан с волной определенной длины. Это, в свою очередь, означает, что волновой пакет должен состоять из волн разной длины. Точно так же, если частица описывается волной определенной длины, такая волна должна быть бесконечной. Кажется, нас подталкивают к выводу, что небольшой волновой пакет состоит из многих бесконечных волн разной длины. И действительно, нас побуждают двигаться по этому пути, и то, что мы описываем, хорошо знакомо математикам, физикам и инженерам. Мы входим в область математики, известную как анализ Фурье и названную в честь французского физика Жозефа Фурье.
Фурье был колоритной личностью. Среди его многочисленных достижений – губернаторство в Нижнем Египте при Наполеоне и открытие парникового эффекта. По слухам, ему нравилось заворачиваться в простыни, что в итоге привело к его безвременной кончине в 1830 году, когда он, плотно завернувшись, упал с собственной лестницы. Его главная аналитическая работа касалась теплопроводности твердого тела и была опубликована в 1807 году, хотя основная идея известна с гораздо более раннего времени.