Фурье показал, что абсолютно любая волна сколь угодно сложной формы и любого размера может быть получена сложением ряда волн-синусоид разной длины. Лучше всего показать это с помощью иллюстрации. На рис. 5.4 пунктирная кривая получается при сложении двух первых волн-синусоид на нижних графиках. Вы можете сложить их едва ли не в уме: обе волны имеют максимальную высоту в центре, так что складываются именно там, а на концах гасят друг друга. Штриховая кривая – это результат сложения всех четырех волн, показанных на нижних графиках, и в ней пик в центре еще более выражен. Наконец, непрерывная кривая показывает, что произойдет при сложении первых десяти волн, то есть четырех приведенных на иллюстрации плюс еще шести с последовательно уменьшающейся длиной. Чем больше мы добавляем волн, тем больше подробностей можем увидеть в результате. Волновой пакет на верхнем графике может описать локализованную частицу, в отличие от волнового пакета, изображенного на рис. 5.3. Таким образом, появляется реальная возможность синтезировать волну любой формы – и все это с помощью сложения простых волн-синусоид.
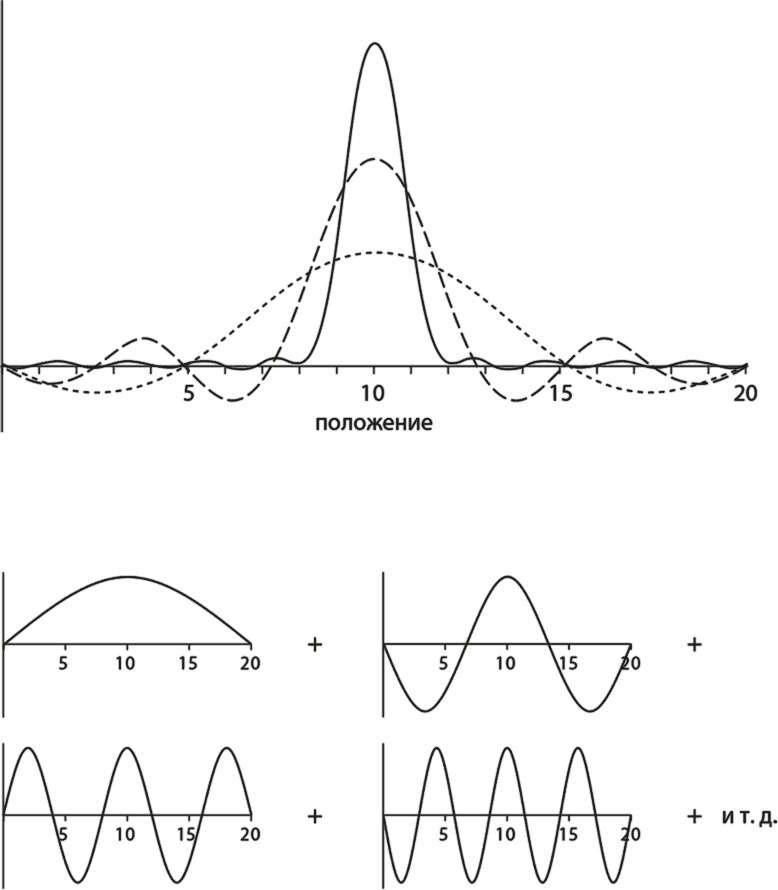
Рис. 5.4. Верхний график: сложение нескольких волн-синусоид дает в результате волновой пакет с резким пиком. Пунктирная кривая состоит из меньшего количества волн, чем штриховая, а та, в свою очередь, из меньшего, чем непрерывная. Нижние графики: первые четыре волны составляют волновой пакет на верхнем графике
Уравнение де Бройля сообщает нам, что каждая волна на нижних графиках рис. 5.4 соответствует частице с определенным импульсом, и этот импульс увеличивается с уменьшением длины волны.
Теперь становится более понятно, почему частица, описываемая локализованной группой циферблатов, должна обязательно иметь диапазон импульсов.
Продолжим пояснения и предположим, что частица описывается группой циферблатов, представленных непрерывной кривой на верхнем графике рис. 5.4
[18]. Мы только что выяснили, что эту частицу можно описать и рядом гораздо более длинных групп циферблатов: первая волна с нижнего графика, плюс вторая волна с нижнего графика, плюс третья волна с нижнего графика и т. д. В этом случае в каждой точке оказывается несколько циферблатов (по одному из каждой длинной группы), которые мы должны сложить, чтобы получился единичный циферблат, представленный на верхнем графике рис. 5.4. Выбор метода представления частицы полностью зависит от вас: можно считать, что она представлена одним циферблатом в каждой точке (в этом случае размер циферблата непосредственно поясняет, где вероятнее всего обнаружить частицу, а именно в окрестности пика верхнего графика рис. 5.4). Или же можно считать, что она описывается как математический ряд циферблатов в любой точке, каждый из которых соответствует одному из возможных значений импульса частицы. Таким способом разложения в ряд мы напоминаем себе, что частица, локализованная в небольшой области пространства, не имеет определенного импульса. Невозможность построить компактный волновой пакет из волн одной-единственной длины – очевидная особенность математики Фурье.
Такой образ мысли дает возможность по-новому взглянуть на принцип неопределенности Гейзенберга. Он утверждает, что мы не можем описать частицу как локализованную группу циферблатов, если эти циферблаты соответствуют волнам только одной длины. Напротив, чтобы циферблаты отменяли друг друга за пределами локализованной области, мы обязаны смешивать волны разной длины, а следовательно, и разного импульса. Итак, цена, которую мы платим за локализацию частицы в какой-то области пространства, состоит в том, что мы не знаем ее импульса. Более того, чем сильнее мы ограничиваем область возможного местоположения частицы, тем больше волн разной длины нужно добавлять и тем хуже мы знаем импульс частицы. Именно это и составляет содержание принципа неопределенности, и очень приятно, что мы пришли к тому же выводу иным путем
[19].
Завершая эту главу, мы хотели бы еще немного поговорить об анализе Фурье. Это очень хорошее средство описания квантовой теории, и оно тесно связано с идеями, которые мы как раз обсуждаем. Важно, что каждая квантовая частица, что бы она ни делала, описывается волновой функцией. Как мы уже говорили, волновая функция – это просто ряд небольших циферблатов, по одному для каждой точки в пространстве, – а размер циферблата определяет вероятность нахождения частицы в конкретной точке. Такой метод представления частицы носит название волновой функции пространственного положения, поскольку непосредственно связан с возможными положениями, которые может иметь частица. Однако есть много вариантов математического представления волновой функции, и маленькие циферблаты в пространственной версии – лишь один из них. Мы уже касались этого вопроса, когда говорили, что можно представить частицу в виде суммы волн-синусоид. Если ненадолго задержаться на этой возможности, легко понять, что составление полного списка волн-синусоид действительно дает исчерпывающее описание частицы (потому что при сложении этих волн можно получить циферблаты, связанные с волновой функцией пространственного положения).
Иными словами, если мы точно укажем, какие именно волны-синусоиды нужны нам для построения волнового пакета и с каким коэффициентом нужно прибавить каждую из волн-синусоид, чтобы получить нужную форму пакета, у нас получится иное, но полностью эквивалентное описание волнового пакета. Интересно, что любая волна-синусоида сама может быть описана одиночным воображаемым циферблатом: его размер отражает максимальную высоту волны, а фаза волны в определенной точке может быть представлена временем, на которое указывает стрелка. Таким образом, мы можем предпочесть представление частицы не через циферблаты в пространстве, но через альтернативный набор циферблатов – по одному для каждого возможного значения импульса частицы. Это описание столь же экономично, как и представление «циферблатов в пространстве», и вместо указания наиболее вероятного положения частицы мы указываем наиболее вероятные значения ее импульса. Этот альтернативный ряд циферблатов называется волновой функцией пространства импульсов и содержит ровно ту же информацию, что и волновая функция пространства положений
[20].
Возможно, это звучит очень абстрактно, но технология, основанная на идеях Фурье, успешно используется в повседневной жизни: разложение волны на составляющие ее волны-синусоиды – это основа технологии аудио– и видеосжатия. Представьте себе звуковые волны, образующие вашу любимую мелодию. Эта сложная волна, как мы уже знаем, может быть разбита на составляющие с помощью ряда чисел, которые показывают относительный вклад каждой из множества волн-синусоид в получающийся звук. Оказывается, что, хотя для абсолютно точного воспроизведения исходного звука требуется множество отдельных волн-синусоид, можно отказаться от многих из них, что совершенно не скажется на восприятии качества аудиозаписи. Например, удаляются волны-синусоиды от звуков, не воспринимаемых человеческим слухом. Это существенно сокращает количество данных, которые нужны для хранения аудиофайла, поэтому ваши mp3-плееры не очень большие.



