Там мы видели, что любой волновой пакет может состоять из сочетания волн определенной длины. Эти особые волны, отражающие состояние частицы с определенным импульсом, – синусоиды. В случае с запертыми водяными волнами можно сделать обобщение, что любое возмущение воды всегда можно описать с помощью какого-то сочетания стоячих волн. Позже в этой главе мы увидим, что стоячие волны имеют в квантовой теории важную интерпретацию: собственно говоря, в них содержится ключ к пониманию строения атома. Держа это в уме, рассмотрим стоячие волны более пристально.
На рис. 6.2 показан еще один пример стоячих волн в природе – три из множества возможных стоячих волн на гитарной струне. Когда мы трогаем гитарную струну, мы слышим звук, который определяется стоячей волной наибольшей длины – первой из трех, показанных на рисунке. И в физике, и в музыке это известно под названием низшей гармоники, или основного тона. Волны другой длины обычно тоже присутствуют и называются обертонами, или высшими гармониками.
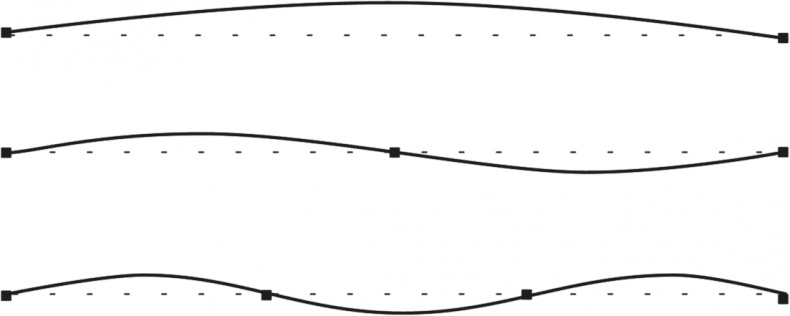
Рис. 6.2. Три волны наибольшей длины, которые могут возникнуть при переборе гитарной струны. Самая длинная волна (сверху) соответствует нижней гармонике (основному тону), а остальные – высшим гармоникам (обертонам)
Две другие волны на рисунке – это два обертона с наибольшими длинами волн.
Гитара – отличный пример: довольно легко понять, почему гитарная струна может вибрировать только на этих конкретных волнах. Дело в том, что она фиксирована на обоих концах: с одной стороны – кобылкой
[22], а с другой – пальцами, прижимающими струну к грифу. Это значит, что в двух этих точках струна не может двигаться, что и определяет разрешенные длины волны. Если вы играете на гитаре, вы инстинктивно понимаете такую физику: перебирая пальцами по грифу по направлению к кобылке, вы уменьшаете длину струны, тем самым заставляя ее колебаться с меньшей длиной волны, что соответствует более высоким нотам.
Нижняя гармоника – это волна, которая имеет всего две стационарные точки, или «узла»; во всех остальных точках она движется. Как видно на рисунке, длина волны звука равна двойной длине струны. Следующая, меньшая длина волны уже равняется длине струны, потому что мы можем видеть еще один узел в центре. Затем можно получить волну с длиной в ⅔ длины струны и т. д.
В целом, как и в случае с водой, запертой в бассейне, струна будет вибрировать в каком-то сочетании различных возможных стоячих волн, в зависимости от того, как именно тронута струна. Конкретную форму струны всегда можно получить, сложив стоячие волны, соответствующие каждой из имеющихся гармоник.
Гармоники и их относительные размеры дают характерный тон звука. У разных гитар будет разное распределение гармоник, поэтому и звучать они будут по-разному, но среднее до (чистая гармоника) на одной гитаре практически совпадает со средним до на другой.
Для гитары форма стоячих волн очень проста: это чистые синусоиды, и их длина фиксирована длиной струны. Для случая с бассейном стоячие волны более сложные, что показано на рис. 6.1, но общая идея такая же.
Возможно, вас интересует, почему эти конкретные волны называются стоячими. Дело в том, что они не меняют своей формы. Если мы сделаем два снимка гитарной струны, колеблющейся в форме стоячей волны, то эти две фотографии будут отличаться только общим размером волны. Пики будут всегда находиться в одних и тех же местах, как и узлы, которые фиксируются концами струны или, в случае с бассейном, его бортиками.
С математической точки зрения можно сказать, что волны на двух фотографиях отличаются только общим множителем. Этот множитель периодически колеблется со временем и отражает ритмические колебания струны. То же самое верно и для бассейна на рис. 6.1, где каждая фотография отличается от остальных общим множителем. Например, последняя фотография может быть получена из первой посредством умножения высоты волны в каждой точке на −1.
Иными словами, волны, каким-то образом ограниченные, всегда можно выразить в виде суммы стоячих волн (то есть тех, которые не меняют своей формы), и, как мы уже сказали, есть довольно серьезные причины посвятить им столько времени. Главная из них – стоячие волны квантованы. Это совершенно очевидно для стоячих волн на гитарной струне: длина основного тона в два раза превышает длину струны, а следующая по длине возможная волна равняется длине струны. Между этими двумя волнами стоячей волны с какой-либо промежуточной длиной быть не может, так что можно сказать, что разрешенные длины волн на гитарной струне квантованы.
Таким образом, с помощью стоячих волн проявляется следующее: «запирая» волны, мы что-то квантуем. В случае с гитарной струной это, очевидно, длина волны. В случае с электроном внутри ящика квантовые волны, соответствующие электрону, тоже будут заперты, и по аналогии можно ожидать, что в ящике будут присутствовать лишь волны с определенным, конкретным набором длин волн, а, следовательно, нечто вновь будет квантовано. Другие волны просто не могут существовать, как гитарная струна не может одновременно звучать всеми нотами в октаве. И общее состояние электрона, как и звук гитары, описывается смешением стоячих волн. Эти квантовые стоячие волны начинают выглядеть очень интересно. Заинтригованы? Приступаем к анализу.
Чтобы продвинуться в своих исследованиях, мы должны уточнить форму ящика, в который помещаем наш электрон. Для простоты предположим, что электрон может свободно двигаться в области размером L, но ему полностью запрещено выходить за пределы этой области. Необязательно уточнять, каким образом мы собираемся запретить электрону это делать, но, если наша модель претендует на то, чтобы быть упрощенной моделью атома, нужно представить, что за это отвечает притяжение положительно заряженного ядра. На научном жаргоне это имеет название «прямоугольная потенциальная яма». Мы зарисовали эту ситуацию на рис. 6.3, и причины для такого названия представляются очевидными. Идея заключения частицы в потенциальной яме очень важна, мы обратимся к ней еще не раз, поэтому полезно убедиться, что мы точно понимаем, о чем идет речь. Как на самом деле можно улавливать частицы?
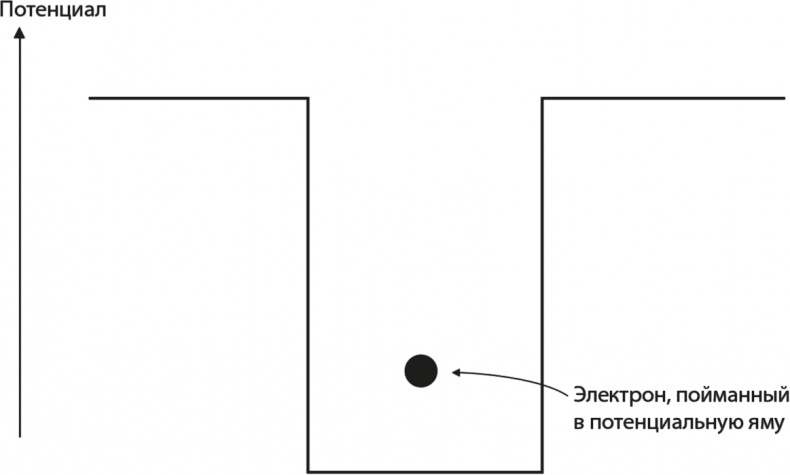
Рис. 6.3. Электрон, пойманный в прямоугольную потенциальную яму
Вопрос довольно сложный: чтобы добраться до его сути, нужно выяснить, как частицы взаимодействуют друг с другом, о чем пойдет речь в главе 10. Тем не менее мы можем добиться прогресса в рассуждениях, если не будем задавать слишком много вопросов.




