Можно еще раз проиллюстрировать это положение с помощью мяча в долине с рис. 6.4. Начнем с мяча, который счастливо покоится на дне. С ним ничего не происходит
[26]. Чтобы заставить мяч катиться вверх по склону, его нужно ударить, то есть добавить ему энергии. В мгновение, следующее за ударом, вся его энергия будет кинетической. По мере подъема мяча по склону он будет замедляться, пока на какой-то высоте не остановится, после чего будет снова падать. В момент остановки он не будет обладать кинетической энергией, но ведь энергия не исчезла по волшебству. На самом деле вся кинетическая энергия превратилась в потенциальную, которая равняется mgh, где g – ускорение свободного падения у поверхности Земли, а h – высота мяча над земной поверхностью. Когда мяч начинает падать, эта накопленная потенциальная энергия при наборе скорости постепенно снова превращается в кинетическую. Итак, пока мяч перелетает с одного конца долины в другой, общая энергия остается постоянной, но периодически перетекает из кинетической в потенциальную. Разумеется, импульс мяча постоянно меняется, но суммарная энергия остается неизменной (предположим, что трения, замедляющего скорость мяча, не существует. Если бы мы включили его в нашу картину, общая энергия тоже осталась бы неизменной, но нужно было бы добавить в качестве ее составляющей энергию, идущую на трение).
Сейчас мы попытаемся исследовать связь между стоячими волнами и частицами определенной энергии иным способом, не обращаясь к особому случаю прямоугольной ямы. Воспользуемся на сей раз маленькими квантовыми циферблатами.
В первую очередь заметьте: если электрон в какой-то момент времени описывается стоячей волной, то он будет описываться той же стоячей волной и в любой следующий момент. Под «той же» мы подразумеваем неизменность формы волны, как в случае со стоячей водяной волной на рис. 6.1. Мы, конечно, не имеем в виду, что волна вообще не меняется: изменяется ее высота, но не положение пиков и узлов.
Это позволяет нам установить, как должно выглядеть описание стоячей волны в терминах квантовых циферблатов, и оно показано на рис. 6.6 для случая стоячей волны основного тона. Размеры циферблатов вдоль волны отражают положение пиков и узлов, а все стрелки часов движутся с одинаковой скоростью. Надеемся, вы понимаете, почему мы изобразили именно такую группу циферблатов. Узлы должны всегда быть узлами, а пики – пиками, и они все должны оставаться на одном месте. Это значит, что циферблаты вблизи узлов должны всегда быть очень маленькими, а циферблаты, соответствующие пикам, должны всегда иметь самые длинные стрелки. Таким образом, единственное, что мы вольны делать, – так это поместить циферблаты по своему усмотрению и заставить их стрелки вращаться синхронно. Если следовать методологии предыдущих глав, мы должны были бы начать с конфигурации циферблатов, показанной в верхнем ряду рис. 6.6, и использовать правила уменьшения и поворота стрелок, чтобы получить три нижних ряда позже. Это упражнение со скачущими циферблатами – слишком сильный скачок прочь от темы книги, но его можно выполнить, и тут есть неплохой поворот
[27], поскольку, чтобы выполнить упражнение правильно, нужно учесть тот факт, что частица «отскакивает от стенок ящика», прежде чем двинуться в своем направлении. Кстати, поскольку циферблаты в центре больше, мы можем непосредственно заключить, что электрон, который описывается этим набором циферблатов, скорее окажется в центре ящика, чем по краям.
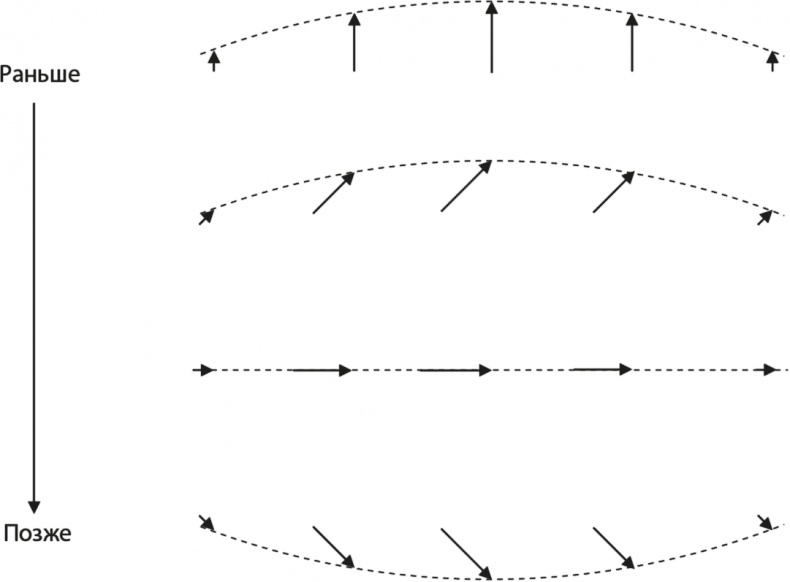
Рис. 6.6. Четыре снимка стоячей волны в последовательные моменты времени. Стрелки на рисунке соответствуют стрелкам часов, а пунктирная линия – проекции «двенадцатичасового» направления. Все стрелки движутся в унисон
Итак, мы выяснили, что удерживаемый электрон описывается набором циферблатов, все стрелки которых вращаются с одинаковой скоростью. Физики, впрочем, обычно так не говорят, а уж музыканты и подавно; те и другие говорят, что стоячие волны – это волны определенной частоты
[28]. Высокочастотные волны соответствуют часам, стрелки которых вращаются быстрее, чем стрелки часов низкочастотных волн. Это понятно, потому что если стрелка часов вращается быстрее, то уменьшается время падения волны с максимума до минимума и обратного подъема (представленного полным оборотом стрелки). Если говорить о водяных волнах, то высокочастотные стоячие волны поднимаются и опускаются быстрее, чем низкочастотные. В музыке говорят, что среднее до имеет частоту 262 Гц, то есть гитарная струна ежесекундно колеблется 262 раза. Нота ля выше среднего до, она имеет частоту 440 Гц, то есть колеблется быстрее (это общепринятый стандарт настройки в большинстве оркестров и для музыкальных инструментов во всем мире). Как мы уже отметили, однако, лишь для чистых синусоид верно, что волны определенной частоты имеют и определенную длину волны. В общем же случае частота – фундаментальная величина, которая описывает стоячие волны, но это определение, кажется, ничего не определяет. Вот вопрос на миллион долларов: что такое электрон определенной частоты? Напомним, что состояния электрона нам интересны, потому что они квантованы, и еще потому, что электрон в одном подобном состоянии остается таким все время (пока нечто не войдет в область потенциала, воздействуя на этот электрон).
Последнее предложение намекает, что мы должны понять значение частоты. В этой главе мы уже встречались с законом сохранения энергии, и это один из самых несомненных законов физики. Сохранение энергии означает, что если электрон в атоме водорода (или в прямоугольной яме) обладает определенной энергией, то эта энергия не может измениться, пока «что-то не произойдет». Иными словами, электрон не может спонтанно изменить свою энергию без какой-либо причины. Кажется, что это не очень интересно, но сравните это со случаем, когда известно, что электрон находится в определенной точке. Как мы все хорошо знаем, он теперь будет перемещаться по всей Вселенной в долю секунды, переводя бесконечное число циферблатов. Но поведение циферблатов для стоячей волны будет иным. Структура циферблатов сохранит свою форму, и все стрелки будут счастливо вращаться, пока что-либо не нарушит их хода. Неизменная природа стоячих волн, таким образом, делает их очевидным кандидатом на описание электрона с определенной энергией.
Сделав шаг, связывающий частоту стоячей волны с энергией частицы, теперь мы можем использовать наше представление о гитарных струнах и предположить, что более высокие частоты должны соответствовать большим энергиям. Дело в том, что высокая частота подразумевает меньшую длину волны (поскольку короткие струны вибрируют быстрее), и мы, изучив конкретный случай прямоугольной потенциальной ямы, можем ожидать, что более короткая длина волны соответствует частице с большей энергией – по уравнению де Бройля. Таким образом, можно сделать важный вывод, который необходимо запомнить: стоячие волны описывают частицы с определенной энергией, и чем больше энергия, тем быстрее идут стрелки часов.



