Что мы знаем о разрешенной энергии электронов в двух атомах? Для общей идеи можно обойтись без вычислений – тем, что мы уже знаем. Если протоны находятся очень далеко друг от друга (например, в нескольких километрах), то самая низкая разрешенная энергия для электронов должна обязательно соответствовать ситуации, когда они связаны с протонами и образуют два изолированных атома водорода. В этом случае велик соблазн сделать вывод, что самое низкое энергетическое состояние для всей системы с двумя протонами и двумя электронами будет соответствовать двум атомам водорода, которые находятся в своих самых низких энергетических состояниях и полностью игнорируют друг друга. Но каким бы верным это ни казалось, на самом деле это не может быть верным. Мы должны мыслить о системе в целом, а эта система из четырех частиц, как и изолированный атом водорода, должна иметь собственный уникальный спектр разрешенных энергий электрона. И принцип Паули подсказывает, что электроны не могут одновременно быть на совершенно одинаковом энергетическом уровне вблизи каждого протона, находясь в блаженном неведении по поводу существования друг друга
[36].
Кажется, мы должны заключить, что пара идентичных электронов в двух отдаленных атомах водорода не может обладать одинаковой энергией, но мы также сказали, что ожидаем нахождение электронов на самом низком энергетическом уровне, соответствующем идеализированному, полностью изолированному атому водорода. Оба этих утверждения не могут быть истинными, и, немного подумав, можно понять, каким должен быть выход из положения: в идеализированном и изолированном атоме водорода должны быть два энергетических уровня, а не один, как мы предполагали изначально. Таким образом мы сможем уместить на нем два электрона и не нарушить принципа Паули. Разница между этими двумя энергиями должна быть очень мала, если атомы сильно удалены друг от друга, так что мы можем представить, что атомы не обращают друг на друга внимания. Но на самом деле они не забывают о существовании друг друга, и все из-за вездесущего принципа Паули: если один из электронов находится в одном энергетическом состоянии, то второй электрон должен пребывать в другом, отличном от первого, энергетическом состоянии, и эта тесная связь между двумя атомами сохраняется независимо от того, насколько они удалены друг от друга.
Та же логика распространяется не только на систему из двух атомов: если по Вселенной рассеяны 24 атома водорода, то на каждое энергетическое состояние в мире единственного атома будет приходиться 24 энергетических состояния, принимающих схожие, но не равные друг другу значения. Когда электрон в одном из атомов занимает некое конкретное состояние, он при этом «знает» все состояния оставшихся 23 электронов, как бы далеко те ни находились. Итак, каждый электрон во Вселенной осведомлен о состоянии каждого другого электрона. И останавливаться на электронах необязательно: протоны и нейтроны тоже можно считать фермионами, так что каждый протон знает о других протонах и каждый электрон знает о других электронах. Связь между частицами, из которых состоит наша Вселенная, настолько тесна, что распространяется на всю Вселенную. Связь эта эфемерна в том смысле, что для сильно отдаленных частиц разница энергий настолько мала, что не оказывает сколь-нибудь существенного воздействия на нашу повседневную жизнь.
Это одно из самых странно звучащих утверждений, к которым мы пришли на страницах книги. Кажется, что заявление о взаимосвязи каждого атома во Вселенной с каждым другим – это брешь, через которую может прорваться всякая холистическая бессмыслица. Но на самом деле здесь нет ничего, с чем бы мы не встречались до этого. Вспомните прямоугольную потенциальную яму, рассматриваемую в главе 6. Ширина ямы определяет разрешенный спектр энергетических уровней, и с изменением размера ямы изменяется и спектр энергетических уровней. То же верно и в данном случае: форма ямы, в которой находятся наши электроны, а следовательно, энергетические уровни, которые им разрешено занимать, определяется положением протонов. Если протонов два, то энергетический спектр определяется положением обоих. А если мы имеем дело с 1080 протонов, формирующих Вселенную, то положение любого из них влияет на форму ямы, в которой находятся 1080 электронов. Существует лишь один набор энергетических уровней, и когда что-то меняется (например, электрон переходит с одного энергетического уровня на другой), то все остальное должно немедленно перестроиться, так чтобы ни одна пара фермионов не оказалась на одинаковом энергетическом уровне.
Идея о том, что электроны немедленно «узнают» все друг о друге, на первый взгляд противоречит теории относительности Эйнштейна. Возможно, мы можем создать какой-то сигнальный аппарат, который будет использовать эти моментальные коммуникации для перемещения информации на скорости выше скорости света. Эта, казалось бы, парадоксальная черта квантовой теории впервые получила оценку в 1935 году – Эйнштейном вместе с Борисом Подольским и Натаном Розеном: Эйнштейн назвал ее «зловещими действиями на расстоянии» и в целом невзлюбил. Прошло определенное время, прежде чем физики осознали, что, несмотря на всю зловещесть, для переноса информации быстрее скорости света эти дальнобойные соответствия использовать нельзя, так что закону причинно-следственных связей ничто не угрожает.
Подобное нездоровое умножение энергетических уровней происходит не по каким-то эзотерическим причинам – это физическое обоснование химических связей. Кроме того, это ключевая причина того, почему одни материалы проводят электричество, а другие нет, а также подспорье в объяснении работы транзистора. Начнем наш путь к транзистору с возвращения к тому «упрощенному» атому, который известен нам из главы 6, где электрон удерживался в потенциальной яме. Эта простая модель не давала возможности верно вычислить энергетический спектр для атома водорода, но научила нас многому в области поведения отдельного атома. Хорошо послужит она и здесь. Возьмем две соединенные прямоугольные ямы и сделаем из них модель двух смежных атомов водорода. Сначала обсудим случай движения одиночного электрона в потенциале, созданном двумя протонами. Верхняя иллюстрация на рис. 8.1 показывает происходящее. Потенциал остается ровным, а потом ныряет вниз, образуя две ямы, что соответствует воздействию двух протонов, удерживающих электроны. Достаточный отступ в центре позволяет удерживать электрон и в левую, и в правую сторону. На техническом жаргоне говорят, что электрон движется в двухъямном потенциале.
.
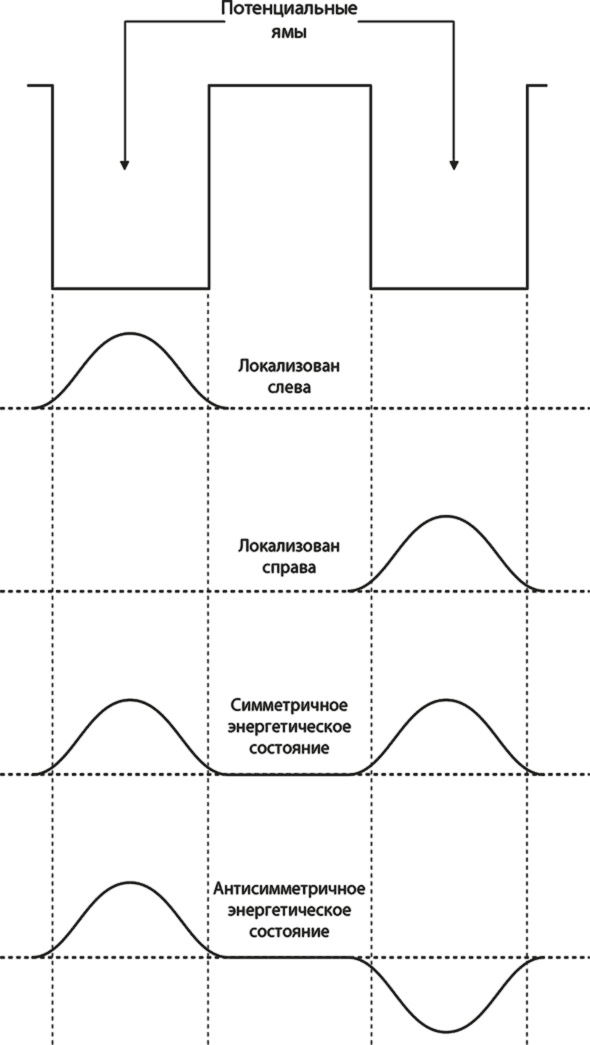
Рис. 8.1. Сверху изображен двухъямный потенциал, а снизу – четыре интересные волновые функции, описывающие электрон в этом потенциале. Только две нижние функции соответствуют электрону с определенной энергией
Наша первая задача – с помощью этой модели понять, что происходит, когда мы сводим два атома водорода: мы увидим, что, когда они в достаточной мере сближаются, образуется молекула. После этого поразмышляем над системами, состоящими более чем из двух атомов, что позволит оценить, что происходит внутри твердого тела. Если ямы очень глубоки, можно воспользоваться результатами из главы 6 и определить, чему должны соответствовать наименьшие электронные состояния. Для одиночного электрона в одиночной прямоугольной яме самое низкое электронное состояние описывается волной-синусоидой, длина которой в два раза превышает размер ящика. Следующему за ним состоянию соответствует синусоида, равная по длине размеру ящика, и т. д. Если поместить электрон в одну часть двойной ямы и если эта яма достаточно глубока, разрешенные энергии должны быть близки по значению к значениям для электрона, удерживаемого в одиночной глубокой яме, так что волновая функция будет очень напоминать синусоиду.



