Сейчас мы сделаем то, что может изначально показаться слишком сложным, но, конечно, имеет под собой серьезные основания. Придется задействовать несколько А, В и Т – иными словами, мы снова возвращаемся на поле твидовых жилетов и меловой пыли; не беспокойтесь, это ненадолго.
Когда частица из точки А в нулевое время направляется к точке В во время Т, мы можем подсчитать, как будет выглядеть циферблат в точке В, переведя стрелки в точке А назад на величину, определенную расстоянием между В и А и временным интервалом. Иными словами, можем записать, что циферблат в точке В задается C(A, 0) P(A, B, T), где C(A, 0) представляет исходный циферблат в точке А и в нулевое время, а P(A, B, T) – воплощение правила перевода и уменьшения циферблатов, связанного со скачком из А в В
[44]. Мы будем называть P(A, B, T) «пропагатором» (функцией распространения. – Прим. ред.) перемещения из точки А в точку В. Теперь, когда известно правило перемещения из точки А в точку В, мы готовы вычислить вероятность нахождения частицы в точке Х. На рис. 4.2 есть множество исходных точек, так что нам придется продвинуться в точку Х из всех этих стартовых точек и сложить все получившиеся циферблаты. В нашей кажущейся зубодробительной нотации получается циферблат C(X, T) = C(X1, 0) P(X1, X, T) + C(X2, 0) P(X2, X, T) + C(X3, 0) P(X3, X, T) +…, где X1, X2, X3 и так далее отражают все позиции частицы в нулевое время (то есть позиции кружков на
рис. 4.2). Уточним: запись C(X3, 0) P(X3, X, T) просто значит «взять циферблат в точке Х3 и переместить ее в точку Х за время Т». Не стоит думать, что тут происходит нечто очень сложное. Все, что мы делаем, так это вкратце записываем то, что уже знаем: «взять циферблат в точке Х3 в нулевое время и рассчитать, насколько перевести стрелки и уменьшить циферблат в соответствии с путем частицы из точки Х3 в точку Х в некоторое более позднее время Т, а затем повторить процесс для всех остальных циферблатов в нулевое время и, наконец, сложить все циферблаты вместе по правилу сложения циферблатов». Уверены, вы согласитесь, что это слишком многословно, поэтому с сокращенной записью жить будет проще.
Мы имеем право считать, что пропагатор воплощает правило перевода и уменьшения циферблатов. Мы можем также считать пропагатор циферблатом. Чтобы оправдать это бессодержательное заявление, представьте, что мы с уверенностью знаем, что электрон находится в точке А во время Т = 0 и что эта ситуация описывается циферблатом размера 1, показывающем 12 часов. Мы можем изобразить перемещение с помощью второго циферблата, и его размер совпадает с величиной, на которую должен быть уменьшен исходный циферблат, а время, которое показывает второй циферблат, соответствует величине необходимого перевода часов. Если скачок электрона из точки А в точку В требует уменьшения исходного циферблата в 5 раз и перевода стрелок на 2 часа назад, то пропагатор P(A, B, T) можно представить в виде циферблата, размер которого равняется 1/5 = 0,2, а стрелки которого указывают на 10 часов (то есть переведены на 2 часа назад с 12). Циферблат в точке В получается простым «умножением» исходного циферблата в точке А на циферблат-пропагатор.
Отступление для тех, кто разбирается в комплексных величинах: как C(X1, 0) и C(X2, 0), так и P(X1, X, T), P(X2, X, T) могут быть представлены в виде комплексного числа, и они сочетаются в соответствии с математическими правилами умножения комплексных чисел.
Для тех, кто не разбирается в комплексных величинах: это неважно, потому что описание с помощью циферблатов столь же точно. Мы всего лишь представили слегка иной взгляд на правило перевода циферблатов: можно переводить стрелки и уменьшать циферблат с помощью другого циферблата.
Нам ничто не мешает выработать правило умножения циферблатов, которое будет работать: умножить размеры двух циферблатов (1 × 0,2 = 0,2) и совместить время на этих двух циферблатах таким образом, что стрелки первого циферблата будут переведены на время второго: 12 минус 10, то есть 2 часа. Кажется, что мы где-то слегка переусердствовали, и это определенно не то, что нужно, когда мы имеем дело лишь с одной частицей. Но физики ленивы, так что они не стали бы впадать во все эти сложные рассуждения, если бы это не экономило время и усилия в долгосрочной перспективе. Введенная здесь запись оказывается очень полезным способом следить за всеми переводами и уменьшениями циферблатов, когда мы подойдем к более интересному случаю с несколькими частицами – например, при рассмотрении атома водорода.
Независимо от деталей можно сказать, что в нашем методе подсчета вероятностей нахождения одинокой частицы где-то во Вселенной есть всего два ключевых момента. Во-первых, нужно указать набор исходных циферблатов, заключающих в себе информацию о том, где частица может находиться в нулевое время. Во-вторых, нужно знать пропагатор P(A, B, T), который сам выступает в роли циферблата, заключающего в себе правило перевода и уменьшения для частицы, перескакивающей из точки А в точку В. Если мы знаем, как выглядит пропагатор для любой пары исходных и конечных точек, то мы знаем все, что нужно знать, и можем с уверенностью высчитать величественно скучную динамику Вселенной, содержащей одну частицу. Впрочем, к ней нельзя относиться пренебрежительно, потому что такое простое положение дел слабо запутывается, когда в игру вступает взаимодействие частиц. Введем же его.
На рис. 10.1 графически изображены все ключевые идеи, которые мы хотим здесь обсудить. Это наше первое знакомство с диаграммами Фейнмана – средством расчета профессионального специалиста по физике частиц. Наша задача: найти вероятность обнаружения пары электронов в точках Х и Y в некоторое время Т. Сначала нам сообщается, где электроны находятся в нулевое время, то есть как выглядят исходные поля циферблатов. Это важно, потому что способность ответить на подобный вопрос эквивалентна способности узнать, «что происходит во Вселенной, содержащей два электрона». Кажется, в этом нет особого прогресса, но теперь весь мир у нас в кармане, потому что мы можем узнать, как основные строительные кирпичики природы взаимодействуют друг с другом.
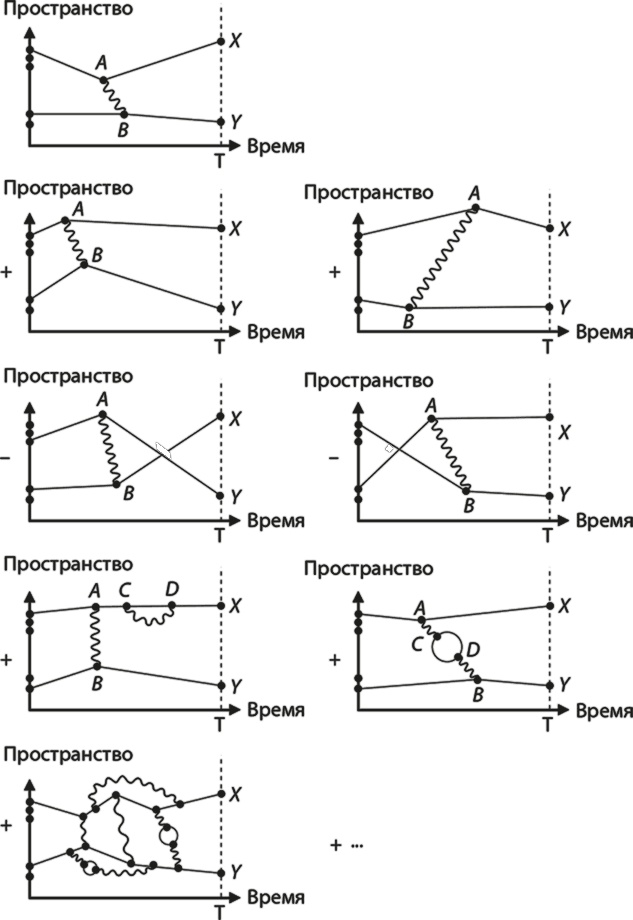
Рис. 10.1. Некоторые способы распада пары электронов. Электроны начинают движение слева и всегда заканчивают его в одной и той же паре точек, X и Y, во время T. Эти графики соответствуют нескольким различным способам, которыми частицы могут достичь точек X и Y



