То, что мы описали, – это самое ядро квантовой электродинамики, другие силы природы можно описать примерно схожим образом. Мы вернемся к этому чуть позже, пока же нужно поговорить кое о чем еще.
Сначала – абзац с описанием двух небольших, но важных деталей. Во-первых, мы упростили суть дела, проигнорировав то, что у электронов есть спин и что они по этому признаку делятся на два типа. Кроме того, спин есть и у фотонов (это бозоны), которые делятся на три типа. Это немного затрудняет вычисления, потому что мы должны следить, с какими типами фотонов и электронов имеем дело на каждой стадии перехода и рассеивания. Во-вторых, если вы внимательно читали, могли заметить знаки минуса перед парой диаграмм на рис. 10.1. Они стоят там, потому что мы говорим об идентичных электронах, перескакивающих из точки Х в точку Y, а две диаграммы со знаками минуса соответствуют взаимному обмену электронов по сравнению с другими диаграммами, то есть электрон, который начал движение из верхнего поля точек, завершает его в точке Y, а второй, нижний электрон оказывается в точке Х. И как мы уже говорили в главе 7, такая смена конфигураций сочетается только после дополнительного перевода циферблата на 6 часов – отсюда и знак минуса.
Не исключено, что вы заметили и возможный недостаток в нашем плане: существует бесконечное количество диаграмм, описывающих варианты перехода частиц из точки Х в точку Y, и суммирование бесконечного количества циферблатов может оказаться, мягко говоря, изнурительным занятием. К счастью, при каждом рассеянии пары электрон – фотон в расчеты входит еще один множитель – g, что уменьшает размер итогового циферблата. Это значит, что чем сложнее диаграмма, тем меньше соответствующий циферблат и тем менее важен он для итогового циферблата. Для квантовой электродинамики величина g довольно мала (около 0,3), так что уменьшение при увеличении числа рассеяний становится намного более явным. Очень часто достаточно учесть только такие диаграммы, как первые пять на рис. 10.1, где рассеяний не более двух, что экономит множество усилий.
Такой процесс вычисления циферблатов (на научном жаргоне известный как «амплитуда») для каждой диаграммы Фейнмана, суммирование всех циферблатов и возведение полученного итогового циферблата в квадрат с целью определения вероятности протекания процесса – это хлеб с маслом современной физики частиц.
Но под поверхностью всего, что мы сказали, таится загадочная проблема, которая очень сильно беспокоит одних физиков и совершенно безразлична другим.
Проблема измерения в квантовой теории
При складывании циферблатов, соответствующих разным диаграммам Фейнмана, появляется эффект квантовой интерференции. Как и в случае с двухщелевым экспериментом, когда нужно было принять во внимание все возможные траектории пути частицы к экрану, мы должны учесть все вероятности перехода пары частиц из исходных положений в окончательные. Это позволяет прийти к правильному ответу, потому что становится возможной интерференция между различными диаграммами. Только в конце процесса, когда все циферблаты просуммированы и все интерференции учтены, нужно возвести в квадрат размер итогового циферблата и вычислить вероятность протекания процесса. Просто. А теперь посмотрите на рис. 10.2.
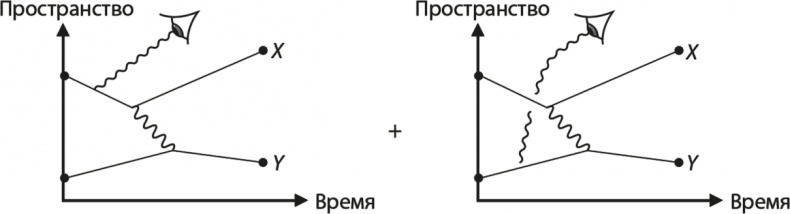
Рис. 10.2. Человеческий глаз смотрит на происходящее
Что случится, если мы попытаемся определить, что делают электроны при перескакивании в точки Х и Y? Единственный способ исследовать, что происходит, – взаимодействовать с системой по правилам игры. В квантовой электродинамике это значит, что мы должны придерживаться правила рассеивания электронов-фотонов, поскольку никаких других правил нет. Итак, попробуем взаимодействовать с одним из фотонов, который может быть испущен одним из двух электронов. Определим его с помощью личного детектора фотонов – собственных глаз. Заметьте, мы задаем теоретически иной вопрос: «Какова вероятность найти электрон в точке Х, другой электрон в точке Y, а также фотон в собственном глазу?» Мы знаем, что сделать для получения ответа: нужно сложить все циферблаты, связанные с различными диаграммами для двух электронов, которые завершаются нахождением одного электрона в точке Х, второго в точке Y и фотона «в собственном глазу». Точнее, мы должны говорить о том, как фотон с этим «моим собственным глазом» взаимодействует.
Хотя все звучит относительно просто, процесс вскоре вырывается из-под контроля. Например, фотон отрывается от электрона, находящегося в одном из атомов моего глаза; это запускает цепочку событий, которая в конечном счете ведет к моему восприятию фотона: я сознательно наблюдаю вспышку света в собственном глазу. Итак, чтобы полностью описать то, что происходит, мы должны определить положение каждой частицы моего мозга, поскольку все они реагируют на появление фотона. И тут мы вплотную подходим к так называемой проблеме измерения в квантовой теории.
До сих пор мы довольно подробно описывали методы вычисления вероятностей в квантовой физике. Под этим понимается, что квантовая теория позволяет вычислить шансы измерения некоего определенного исхода эксперимента. В этом процессе нет никаких двусмысленностей – достаточно следовать правилам игры и не отклоняться от вычисления вероятности того, что может произойти. Однако случается нечто неприятное. Представьте, что ученый проводит эксперимент, для которого возможны лишь два исхода – «да» и «нет». Итак, эксперимент состоялся, и в результате экспериментатор записал исход «да» или «нет», но уж никак не то и другое одновременно. Пока все хорошо.
Теперь представим, что позже второй экспериментатор измеряет нечто другое (что именно – не имеет значения).
Снова примем как данность, что эксперимент прост и возможных исходов два – «есть щелчок» и «нет щелчка». Правила квантовой физики диктуют: мы должны вычислить вероятность того, что второй эксперимент даст «щелчок», просуммировав циферблаты, связанные со всеми вероятностями, ведущими к такому исходу. Это может включать в себя вариант, что первый экспериментатор получает исход «да», и дополняющий его вариант с исходом «нет». Только после суммирования двух исходов мы получим правильный ответ и узнаем, какова вероятность результата «есть щелчок» во втором эксперименте. Но так ли это? Действительно ли нужно принимать в расчет необходимость поддержания связности мира даже после того, как некое измерение завершилось? Или же на самом деле после получения результата «да» или «нет» в первом эксперименте будущее зависит лишь от измерения? Например, во втором эксперименте это значит, что если первый экспериментатор получает «да», то вероятность исхода «есть щелчок» во втором эксперименте должна вычисляться не исходя из суммы вероятностей «да» и «нет», а лишь после учета вероятностей, при которых мир может развиться от «первый экспериментатор получает ответ да» до «второй эксперимент дает щелчок». Разумеется, при этом получится не тот ответ, как при суммировании обоих исходов «да» и «нет», так что, если мы стремимся к полному пониманию, нужно выяснить, как следует поступать.

