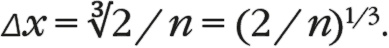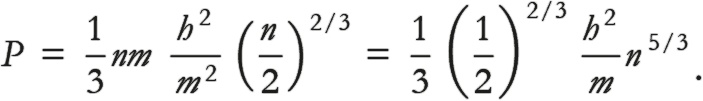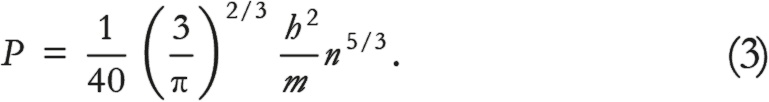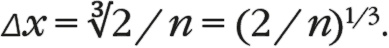
Теперь можно соотнести это с нашим выражением, полученным из принципа неопределенности, и вычислить типичный импульс электронов в соответствии с их квантовыми колебаниями:
где знак ~ означает «примерно равно». Разумеется, уравнение не может быть точным, потому что все электроны никак не могут колебаться одинаково: одни будут двигаться быстрее типичного значения, другие медленнее. Принцип неопределенности Гейзенберга не способен точно сказать, сколько электронов движутся с одной скоростью, а сколько с другой. Он дает возможность сделать более приблизительное утверждение: например, если сжать область электрона, то он будет колебаться с импульсом, примерно равным h / Δx. Мы возьмем этот типичный импульс и положим его одинаковым для всех электронов. Тем самым немного потеряем в точности вычислений, но существенно выиграем в простоте, а физика явления определенно останется той же самой
[58].
Теперь мы знаем скорость электронов, что дает достаточно информации для определения давления, которое они оказывают на наш кубик. Чтобы убедиться в этом, представьте, как целый флот электронов движется в одном и том же направлении с одной и той же скоростью (v) по направлению к прямому зеркалу. Они ударяются о зеркало и отскакивают, двигаясь все с той же скоростью, но на сей раз в обратном направлении. Давайте вычислим силу, с которой электроны действуют на зеркало. После этого можно перейти к более реалистичным вычислениям для случаев, когда электроны двигаются в разных направлениях. Такая методология очень распространена в физике: сначала стоит поразмыслить над более простым вариантом задачи, которую хочешь решить. Тем самым можно разобраться в физике явления с меньшими проблемами и обрести уверенность для решения более серьезной задачи.
Представьте, что флот электронов состоит из n частиц на м³ и для простоты имеет в круглом сечении площадь 1 м², как показано на рис. 12.4. Через секунду nv электронов ударится о зеркало (если v измеряется в метрах в секунду).
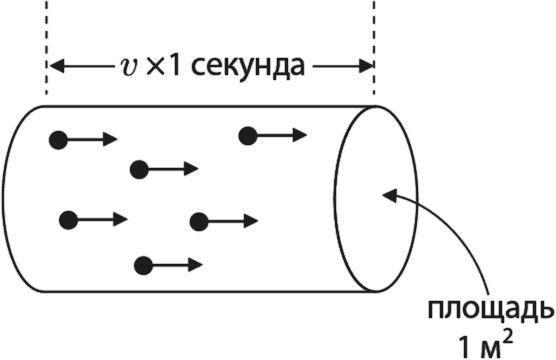
Рис. 12.4. Флот электронов (маленькие точки), движущийся в едином направлении. Все электроны в трубке такого размера будут ежесекундно ударяться о зеркало
Мы знаем это, потому что все электроны, удаленные от зеркала на расстояние v × 1 с, будут ежесекундно врезаться в зеркало. Это относится ко всем электронам в трубке, изображенной на рисунке. Поскольку объем цилиндра равен площади его поперечного сечения, помноженной на длину, то объем трубки равен v м³, а поскольку во флоте электронов на 1 м³ приходится n электронов, значит, ежесекундно в зеркало врезается nv электронов.
Когда каждый электрон отскакивает от зеркала, он получает обратный импульс, то есть каждый электрон изменяет свой импульс на величину 2mv. Сила требуется как для того, чтобы остановить движущийся автобус и отправить его в противоположном направлении, так и для поворота импульса электрона. И тут вновь в игру вступает Исаак Ньютон. В главе 1 мы записали его второй закон в виде F = ma, но вообще-то это частный случай более общего правила, которое гласит, что сила равна изменению импульса
[59]. Итак, все электроны прикладывают к зеркалу общую силу F = 2mv × (nv), потому что именно таково общее ежесекундное изменение импульса электронов. Благодаря тому, что пучок электронов имеет площадь 1 м², таково же будет и давление, оказываемое всеми электронами на зеркало.
От пучка электронов до газа, состоящего из электронов, лишь маленький шаг. Мы должны теперь учесть, что не все электроны движутся в одном направлении: какие-то движутся вверх, какие-то вниз, какие-то направо, какие-то налево и т. д. В результате мы должны разделить давление, оказываемое в любом направлении, на 6 (вспомните о шести гранях куба). Получится (2mv) × (nv) / 6 = nmv² / 3. В этом уравнении v можно заменить типичными скоростями движения электронов, которые мы получили в предыдущем уравнении (2) благодаря принципу неопределенности Гейзенберга, и вычислить общую величину давления, которое оказывают электроны в звезде – белом карлике
[60]:
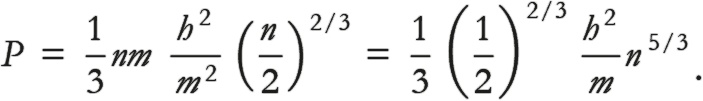
Если помните, мы предупреждали, что это приблизительный результат. Полный результат, для которого требуется гораздо больше математики, таков:
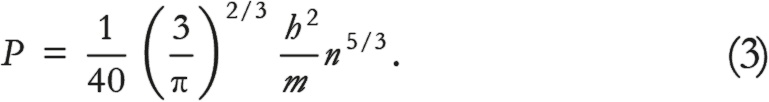
Это отличный результат. Он говорит, что давление в некотором месте звезды варьируется пропорционально количеству электронов на единицу объема в этом месте, возведенном в степень 5/3. Не беспокойтесь о том, что мы не получили константу пропорциональности в этих приблизительных расчетах, – важно, что все сошлось. Мы тем самым сказали также, что наша оценка импульса электронов, вероятно, чуть завышена, что объясняет, почему наша оценка давления оказалась выше истинного значения.
Выражение давления через плотность электронов – хорошее начало, но нашим целям лучше соответствовало бы выразить его через истинную плотность звезды. Это можно сделать, высказав на редкость безопасное предположение, что подавляющее большинство массы звезды приходится на ядра, а не на электроны (масса протона примерно в 2000 раз больше массы электрона). Мы знаем также, что количество электронов в звезде должно равняться количеству протонов, потому что звезда электрически нейтральна. Чтобы получить массовую плотность, мы должны знать, сколько протонов и нейтронов приходится на 1 м³ звезды, при этом о нейтронах забывать нельзя, так как это побочный продукт процесса синтеза. У более легких белых карликов ядро в основном будет состоять из гелия-4, конечного продукта водородного синтеза, а следовательно, количество нейтронов и протонов будет одинаковым. Теперь немного об условных обозначениях. Номер атомной массы А условно используется для обозначения числа протонов и нейтронов в ядре. Для гелия-4 А = 4.